arytmetyka salamandra: Czy umiałby ktoś z Was wytłumaczyć mi podpunkt b) ze zdjęcia jak dodać binarnie jedynkę do tamtej liczby? Wykładowca tłumaczył to na zasadzie rozpisywania możliwych cyfr w danej liczbie, czyli w binarnej (0,1) i później (jak widać w przykładzie a)) jeśli mamy na końcu 0, to jest ono mniejsze od największej możliwej cyfry (1), więc przesuwamy cyfrę jedności o jeden w prawo itd. Jeśli ostatnia cyfra byłaby równa tej największej możliwej (1), to cykl powtórzyłby się do momentu, aż dana cyfra byłaby różna od tej największej możliwej. W drugim przykładzie nie mogę się połapać czemu cykl kończy się dopiero za trzecim razem. Według mnie, dodajemy, więc mamy 2 (binarnie 10), więc zapisujemy 0, a jedynka przechodzi, tak jak w zwykłym dodawaniu pisemnym, więc na drugiej pozycji mamy znowu 2 (binarnie 10), zapisujemy 0, i jedynka z powrotem przechodzi dalej− na trzeciej pozycji mamy 1, no i dalej już przepisujemy. Ale według tego myślenia, to cykl powinniśmy zakończyć w pozycji drugiej, bo już tam cyfra ≠1. Przepraszam, nie potrafię prościej wyjaśnić o co mi chodzi link: https://imgur.com/a/SvZ8rpT

salamandra: Chociaż chyba doszedłem do błędu − tam gdzie mamy trzy linijki pod rząd =1, ≠1, ≠1, to ta druga linijka chyba powinna również być =1, a nie ≠1 i to mnie zmyliło

a7: mamy 1+1=0 pełna "dziesiątka" jeden dalej, następnie 1+1 = 0 pełna dziesiątka 1 dalej, 1+0 =1 i resztę przepisujemy

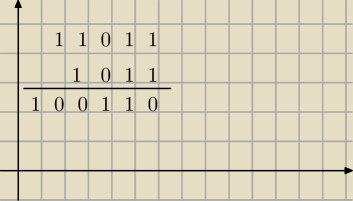
Mila: Nie wiem jakie liczby chcesz dodać. Napisz tutaj, bo tam są bazgroły. Będę po 20.

a7: 101011 + 1 ____________ 101100

salamandra: 101011+1 (w systemie binarnym). Już sobie poradziłem, tak jak napisałem 19:26− zmyliła mnie ta druga linijka, w której powinno być napisane =1. @a7, tak, obliczyć umiem, ale chciałem załapać ten sposób wykładowcy, bo on na dobrą sprawę nic nie dodawał, tylko zawsze coś przesuwał, przy dzieleniu, też nie dzielił, tylko dokonywał przesunięcia bitowego. Nawet jakbym miał dwie liczby binarne do dodania, to nadal wolałbym zamienić je szybko na system dziesiętny i później z powrotem na binarkę, na razie co prawda pokazywał tylko "dodawanie" jedynki.

a7: możesz wpisać w wyszukiwarkę dodawanie w systemie binarnym i jest na wiele sposobów bardzo szybko wytłumaczone to dużo szybsze niż zamienianie na dziesiętny 0 1 0 1 +0 0 1 1 ____ ___ ____ ____ 0 1 1 10

Mila: