Liczba rozwiązań w zależności od parametru PytanieDo: Ile rozwiązań ma rówanie ln(|a−x|)=x w zależności od a? Próbowałem: y=a−x x=a−y 1) ln(y) = a−y y<0 f(y) = ln(−y) = a+y

	1
f'(y) = −		+1
	y

f'(y) >0 y>1 =0 y=1 <0 y<1 f(1)=a−1 a=1 1 rozw. a<1 0 rozw. a>1 2 rozw. y>0

	1
f'(x) =		+1
	y

f'(x) = 0 y=−1 f(−1) = a +1 a = −1 1 rozw. Czy poprawnie?

jc: Zawsze 1 rozwiązanie.

jc: Oj, coś pomyliłem. e^x=|x−a| a=−1, dwa rozwiązania a<−1, trzy rozwiązania a>−1, jedno rozwiązanie

PytanieDo: Mógłbyś bardziej rozpisać, chociaż fragmenty? Nie wiem, w którym miejscu mylę się ze znakiem

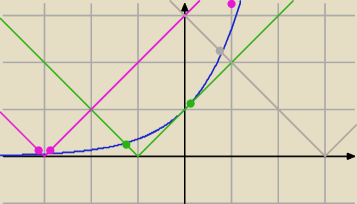
a7: a=−1 zielony kolor− dwa rozwiązania a<−1 (a=−3) różowy kolor − trzy rozwiązania a>−1 (a=3) szary kolor − jedno rozwiązanie

PytanieDo: Bardzo dziękuję za przejrzyste i estetyczne rozpisanie Czy mógłbym również prosić o wskazanie błędu w moim równaniu?

a7: ja mam wątpliwość gdyż jc zamienił kolejność |a−x| na |x−a| i wolałabym , żeby on to sam zweryfikował

a7: w Twoim rozwiązaniu też nie umiem wskazać błędu nie bardzo to rozwiązanie w ogóle rozumiem

Jerzy: 21:10 , |a − b| = |b − a|

a7: ok dzięki

a7: ja napiszesz swoje rozwiązanie z dokładniejszym (słownym) wytłumaczeniem co się z czego wzięło to spróbuję znaleźć ew. błąd jak dam radę

a7: *jak

jc: |a−x|=|x−a| Swoje rozwiązanie odczytałem z rysunku takiego, jak u a7.

ICSP: W ogóle nie wiadomo co robisz w tym twoim rozwiązaniu. Jedyne co udało mi się znaleźć to błąd podczas liczenia pochodnej. Za tego typu rozwiązanie nawet gdyby było poprawne nikt nie da Ci maksymalnej liczby punktów. W przeciwieństwie do matury z j. polskiego tutaj nikt nie będzie się domyślał co autor miał na myśli.

PytanieDo: ICSP, mógłbyś wskazać błąd? ln(|a−x|)=x y=a−x podstawienie do logarytmu, do łatwiejszych obliczeń x=a−y Zamieniam: ln(y) = a−y Wartość bezwzględna nie wpływa na znak rozwiązania, jednak samo x może być ujemne, dlatego rozważam −y oraz y Nie wiem, czy tutaj nie popełniam błędu... Zobaczymy. x=a−y −x=y−a Teraz zmienię strategię nieznacznie x<0 ln(y) = y−a f(y) = ln(y)−y+a

	1
f'(y) =		−1
	y

Przyrównuję do zera, by znaleźć ekstremum, otrzymuję: f'(y) = 0 => y=1 <0 y>1 >0 y<1 Aby f(1)=0, potrzebujemy odpowiedniego a: f(1) = 1−a a=1 Analogicznie x>0 ln(y)=a−y f(y)=ln(y)−a+y

	1
f'(y)=		+y
	y

=0 y=−1 <0 y<−1 >0 y<−1 Teraz, po wypisaniu wszystkiego, istotnie zauważam, że pogubiłem się. Proszę, czy dobra duszyczka przedstawiłaby swoje rozwiązanie za pomocą pochodnych, bez polegania wyłączeni na wykresie?

a7: 1. pierwsza uwaga : trzeba napisać ln|y|

PytanieDo: Dobrze, dziękuję. Następne uwagi?

a7: 2. chyba brak założenia y≠1

a7: bez polegania na wykresie zaraz spróbuję...

a7: nie, jednak nie potrafię....

a7: ale wolfram potrafi zobacz czy przypadkiem nie o takie coś Ci chodziło https://www.wolframalpha.com/input/?i=ln%28%7Ca%E2%88%92x%7C%29%3Dx