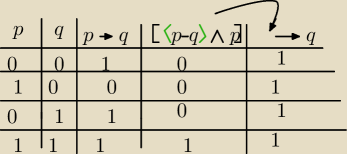
logika salamandra: Udowodnij prawo odrywania [(p⇒q) ⋀ p] ⇒ q Rozumiem, że fakt, iż jest to tautologia jest wystarczający, aby stwierdzić, że jest to prawo? Drugie pytanie− do czego mi w zasadzie może posłużyć to prawo? O ile jakieś prawo daje mi równoważność, to jestem w stanie zrozumieć, że mogę je stosować zamiennie, natomiast co w przypadku, gdy mam prawo z implikacją, tak jak tutaj?

ite: To bardzo ważna tautologia, tak ważne że ma swoją nazwę modus ponendo ponens. Działa na tej zasadzie, co wspinaczka w górach albo przeprawa przez rzekę. Jestem już tutaj /p/ i mam miejsce następny chwyt (kamień na kolejny krok) /p⇒q/. Stawiam te krok i jestem już dalej /q/. Wiem, że prawdziwa jest implikacja p⇒q i wiem że prawdziwe jest zdanie p. Przeprowadzam wnioskowanie dedukcyjne wg podanego schematu i wiem więcej: mam potwierdzenie, że prawdziwe jest również zdanie q.

salamandra: Mogłabyś podać jeszcze jakiś inny przykład, abym lepiej zrozumiał to prawo? Już chyba umiem je udowadniać, ale nie potrafię sobie wytłumaczyć skąd to wynika i właśnie jakie przykłady sobie dobrać do tego

ite: Jeśli dużo ćwiczę, to gram coraz lepiej. Dużo ćwiczę. p⇒q p wniosek / więc prawdą jest że Gram coraz lepiej. q

ite: Z tego, że lepiej pracuję, wynika że więcej zarabiam. Lepiej teraz pracuję. p⇒q ∧ p Zarabiam więcej. q [(p⇒q) ∧ p] ⇒ q

ite: (starodawne ⚓) Nie zna życia, kto nie służył w marynarce. Nie służył w marynarce. Nie zna życia.

salamandra: Super, dziękuję. Na dobrą sprawę, czemu służy to prawo, skoro p→q już wynika, że jak lepiej pracuję, to zarabiam więcej?

ite: Jak lepiej pracuję, to więcej zarabiam (p⇒q). Tylko tyle wiemy. Z tej implikacji nie wynika, jak pracuję, czy lepiej czy nie. Mogę pracować lepiej (p) i modus ponendo ponens − MPP gwarantuje (przy prawdziwych przesłankach), że zarabiam lepiej. Ale mogę też pracować tak samo lub gorzej (¬p) i wtedy nie da się wywnioskować, czy zarabiam więcej czy nie. Jeśli pada, to jest mokro. Z tego nie wynika, że jest mokro, dopóki nie mamy pewności, że pada.

salamandra: Aha, teraz rozumiem, dziękuję jeszcze raz czy z doświadczenia mogłabyś zdradzić, czy muszę znać na pamięć te wszystkie prawa, bo na dobrą sprawę nie wiem jak podejść do nauki logiki, dziś ćwiczyłem metodą zero−jedynkową udowadnianie praw, formuł

ite: Nie ucz się na pamięć, ale jak masz sprawdzić, czy jakaś formuła jest tautologią, to zajrzyj najpierw do jakiegoś zestawienia, np. http://algebra.rezolwenta.eu.org/Materialy/logika-tautologie.pdf . Jak będziesz co jakiś czas czegoś szukać i sprawdzać, to zapamiętasz podstawowe prawa i ich nazwy.

salamandra: Ok, bo nie bardzo wiem, czego mam się spodziewać po tym dziale, jakich zadań, na razie właśnie zajmowałem się tylko udowadnianiem praw lub sprawdzaniem prawidłowości formuł i zastanawiałem się, czy znajomość tych praw "na pamięć" w przyszłości się do czegoś przyda.

ite: Nie chodzi o to żeby wkuwać, ale kojarzyć i umieć odszukać, przydają się przy przeprowadzaniu dowodów w rachunku zdań i w rachunku predykatów.