przedstawienie na płaszczyźnie jaros: √(x−1)² + y² + √(x+1)² + y² = 3 Jak coś takiego przedstawić na płaścinie x,y. Wiem, że to równie okręgu tylko jak znaleźć środek i promień?

a7: to elipsa https://www.wolframalpha.com/input/?i=%E2%88%9A%28%28x%E2%88%921%29%5E2+%2B+y2%29+%2B+%E2%88%9A%28%28x%2B1%29%5E2+%2B+y2%29+%3D+3+

jaros: A masz pomysł jak do tego dojść algebraicznie?

Mila:

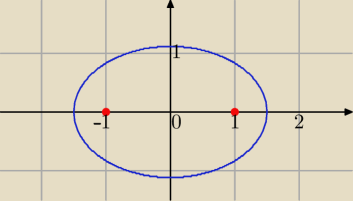
	x2		y2
Elipsa:		+		=1
	a2		b2

Ogniska : F₁=(−1,0), F₂=(1,0) 2c=|F₁F₂|=2 c=1

	3
2a=3 , a=
	2

c²=a²−b²

	3
12=(		)2−b2
	2

	5
b2=
	4

Elipsa:

x2		y2
	+		=1
9   4		5   4

	√5
y=±		*√9−4x2
	6

a7:

	3
√(x−1)2+y2=2*		−√(x+1)2+y2
	2

	3		3
(x−1)2+y2=4*(		)2−4*		*√(x+1)2+y2+(x+1)2+y2
	2		2

	3		3
x2−2x+1+y2=4*(		)2−4*		*√(x+1)2+y2+x2+2x+1+y2
	2		2

	3		3
4*		*√(x+1)2+y2=4*(		)2+4*1*x (c=1) (2a=3, czyli a=3/2)
	2		2

3		3
	*√(x+1)2+y2=(		)2+x
2		2

	3		3		3
(		)2*((x+1)2+y2)=x2+2*(		)2+(		)4
	2		2		2

	3		3		3		3		3		3
(		)2*x2+(		)2*2x+(		)2+(		)2*y2=x2+2*x*(		)2+(		)4
	2		2		2		2		2		2

	3		3		3		3
(		)2*x2+(		)2+(		)2*y2=x2+(		)4
	2		2		2		2

	3		3		3		3
(		)2−1)*x2+(		)2*y2=(		)4−(		)2
	2		2		2		2

	3		3		3		3
(		)2−12)*x2+(		)2*y2=(		)2*((		)2−12)
	2		2		2		2

	3
((		)2−12)=b2
	2

	3		3		3
b2x2+(		)2*y2=b2*(		)2 dzielimy obie strony przez b2*(		)2
	2		2		2

x2		y2
	+		=1
3   ( )2   2		3   )2−12 2

i mamy standardową postać równania elipsy

x2		y2
	+		=1
a2		b2

	√5
czyli a=3/2 (długość półosi wielkiej) b=		(?) (długość półosi małej)
	2

a7: wykład ósmy strona 12 https://www.mini.pw.edu.pl/~figurny/www/?Dydaktyka:SIMR_Algebra_wyk%B3ad