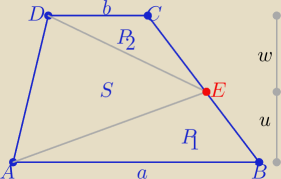
trapez Moris: W trapezie ABCD o podstawach AB i CD , na ramieniu BC wybrano punkt E wiedząc,że pola trójkątów ABE, DCE i ADE są odpowiednio równe P₁,P₂ i S Wykaż,że S≥2√P₁*P₂

Eta:

au

bw

a+b

au

bw

aw+bu

P1=

, P2=

P(ABCD)=

*(u+w) =

+

+

2

2

2

2

2

2

P(ABCD)=P₁+P₂+S

	aw+bu
to S=
	2

z nierówności między średnimi AM≥GM

	aw+bu
S=		≥√aw*bu =√au*bw=√2P1*2P2= 2√P1*P2
	2

S≥2√P₁*P₂ =============

Serce w rozterce : Mozna bez srednich? Dziękuję .

wredulus_pospolitus: Nie można. Proszę

Serce w rozterce : Ok. Wo mingbai (rozumiem)

Moris: Wow dzięki eta