Okrąg wpisany w trapez Matematyk: Wiadomo, że w trapez można wpisać okrąg. Na ramionach tego trapezu, jako na średnicach, konstruujemy okręgi. Pokaż, że powstałe okręgi są styczne zewnętrznie.

tim: Rysuję.

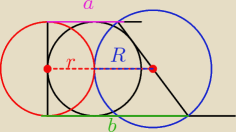
tim: Odcinek r + R łączy środek ramion, zatem jest on równy długości tego odcinka: Mamy wykazać, że:

a + b
	= r + R
2

Wiemy także, że a + b = c + d Wiemy też, że c = 2r, a d = 2R Zatem: a + b = 2r + 2R (a + b)/2 = r + R co należało wykazać.

Matematyk: Dzięki

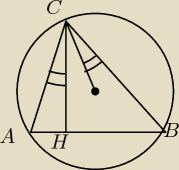
Matematyk: Jeszcze takie jedno. Dany jest trójkąt ostrokątny ABC. Uzasadnij, że |∠ACH|=|∠BCO|, gdzie AH jest wysokością w tym trójkącie i O jest środkiem okręgu opisanego na tym trójkącie(patrz rysunek)

Ozz: Właśnie co z zadankiem powyżej? Jak je rozszyfrować?