Nierówności wymierne i wielomianowe Student: Rozwiązać nierówność: 1. (x⁴ − 4x +1)(x⁴ − 4x +2) ≤ 20 Tutaj zastosowałem podstawianie, t = x⁴ − 4x +1 wyszło mi t<−5, 4> ale potem nie mogę obliczyć nic dalej... 2. (x² + 3x)(3x + 3) − 16(3x+3)/(x² + 3x) ≥ 0 Tutaj dziedzina, i co dalej byście zrobili? Mam kilkanaście takich do rozwiązania. W jaki sposób się je rozwiązuje? Nie sądzę, że robi się to mnożeniem...

wredulus_pospolitus: t = x⁴ − 4x + 1.5

	81		9		9
(t − 0.5)(t + 0.5) = t2 − 0.25 ≤ 20 −> t2 ≤		−−> −		≤ t ≤
	4		2		2

więc masz: x⁴ − 4x + 6 ≥ 0 x⁴ − 4x − 3 ≤ 0 I tyle zrobisz ... chyba że treść jest z goła inna

wredulus_pospolitus: 2. x² + 3x = x(x+3) 3x + 3 = 3(x+1)

	x+1		16
3x(x+1)(x+3) − 16*3		= 3(x+1)[ x(x+3) −		] = (*)
	x(x+3)		x(x+3)

	16		a2 − 16		(a−4)(a+4)
// rozwiążmy problem: a −		=		=
	a		a		a

u nas a = x(x+3) a więc //

	( x(x+3) − 4)( x(x+3) + 4)
(*) = 3(x+1)*		= .... ciągnij dalej
	x(x+3)

Student: Dzięki, drugie udało mi się zrobić, to wystawienie zmieniło postać rzeczy i dalej widzę, że zeruje −4 i 1 https://imgur.com/DO7wurr 1.66 (to jest to pierwsze) Być może tak ma zostać, dzięki!

Mila: 2)

	16(3x+3)
(x2 + 3x)(3x + 3) −		≥ 0 taki zapis,
	(x2 + 3x)

czy taki?

(x2 + 3x)(3x + 3) − 16(3x+3)
(x2 + 3x)

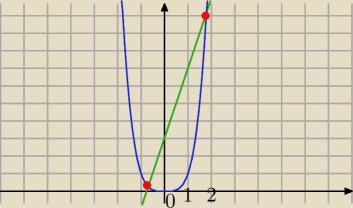
Mila: 1) (x⁴ − 4x +1)(x⁴ − 4x +2) ≤ 20 t=x⁴−4x (t+1)*(t+2)≤20⇔ t²+3t−18≤0 t∊<−6,3> −6≤x⁴−4x≤3 x⁴−4x≥−6 i x⁴−4x≤3 x⁴−4x+6≥0 i x⁴−4x−3≤0 1) f(x)=x⁴−4x+6 f'(x)=4x³−4 4x³−4=0 x³=1 x=1 f_min dla x=1 f(1)=1−4+6=3>0⇔x⁴−4x+6>0 dla x∊R 2) g(x)=x⁴−4x−3 g'(x)=4x³−4 g_min dla x=1 g(1)=1−4−3=−6 3)g(x) ma dwa miejsca zerowe, x₁<1, x₂>1 g(2)=16−8−3=5>0⇔x₂∊(1,2) g(−1)=1+4+6>0 x₁∊(−1,0) [ g(0)=−3] Albo graficznie: x⁴=4x+3 x₁≈−0.7 , x₂≈1.7 Nierówność : x⁴≤4x+3 dla x∊<−1.3, 1,7> w przybliżeniu

Mila: Nierówność : x⁴≤4x+3 dla x∊<−0.7, 1,7> w przybliżeniu

Mariusz: x⁴ − 4x + 6=0 Grupujesz wyrazy x⁴−(4x−6)=0 Ponieważ wyrażenie w drugim nawiasie jest trójmianem kwadratowym wprowadzasz parametr aby uzależnić od niego wartość wyróżnika

	y		y2
(x2+		)2−(yx2+4x+		−6)=0
	2		4

Δ=0

	y2
16−4y(		−6)=0
	4

y(y²−24)−16=0 y³−24y−16=0 y= u+v y³=u³+3u²+3uv²+v³ y³=u³+v³+3uv(u+v) u³+v³+3uv(u+v)−24(u+v)−16=0 u³+v³−16=0 3(u+v)(uv−8)=0 u³+v³=16 uv=8 u³+v³=16 u³v³=512 t²−16t+512=0 (t−8)²+448 y³−24y−16=0 y=ucos(θ)

24u		3
	=
u3		4

32
	=1
u2

u²=32 u=4√2 y³−24y=16 y=4√2cos(θ) 128√2cos³(θ)−96√2cos(θ)=16|:32√2

	√2
4cos3(θ)−3cos(θ)=
	4

	√2
cos(3θ)=
	4

	1		√2
y1=4√2cos(		arccos(		))
	3		4

	1		√2
y2=4√2cos(		(arccos(		)+2π))
	3		4

	1		√2
y2=4√2cos(		(arccos(		)+4π))
	3		4

	y		y2
(x2+		)2−(yx2+4x+		−6)=0
	2		4

	y		4
(x2+		)2−y(x+		)2
	2		2y

	y		4
(x2+		)2−(√yx+		)2
	2		2√y

	1		4		1		4
x4 − 4x + 6=(x2−√yx+		(y−		))(x2+√yx+		(y+		))
	2		√y		2		√y

gdzie

	1		√2
y=4√2cos(		arccos(		))
	3		4

Teraz już będzie łatwiej rozwiązać tę nierówność

Mariusz: "Mam kilkanaście takich do rozwiązania. W jaki sposób się je rozwiązuje? Nie sądzę, że robi się to mnożeniem..." Student przejrzyj sobie pdf http://matwbn.icm.edu.pl/ksiazki/mon/mon11/mon1110.pdf Jeżeli będziesz miał pytania do przedstawionych w tym pdf sposobów to pisz