Równanie DAniel: Wykaż, że jeżeli c,d są liczbami całkowitymi przy czym c≠0 i d>0 to równanie x³ −3cx² −dx+c =0 nie posiada więcej niż jeden pierwiastek wymierny.

a7: funkcja ta ma tylko jeden punkt przegięcia x=c (druga pochodna f''(x)=6x−6c) może to jest trop

a7: żeby równanie to posiadało tylko jeden pierwiastek wymierny to c musi być=1

a7: nie, przepraszam, jednak nie

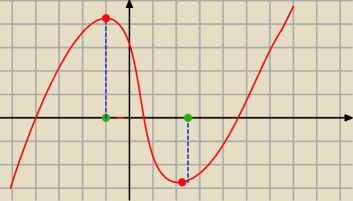
a7: f'(x)=3x²−6xc−d Δ=36+12d √Δ= x₁=1−√1+d/3 x₂=1+√1+d/3 x₁≠0, gdyż d≠0 i x₁<0 a x₂>2 f''(x)=6x−6c f"(x)=0 dla x=c czyli f−cja ma jeden punkt przegięcia w punkcie c, wiemy, że c≠0 założmy, że c>0 wtedy W(0)>0 (gdyż W(0)=c) nie wiem czy te rozważania coś pomogą, ale może ktoś inny wpadnie na jakiś trop

DAniel: dzięki

a7: no ale to coś pomogło?

a7: mam nowy trop, moment

a7: x³−3cx²−dx+c=0 x(x²−d)−3c(x²−1/3c)=0 dla d=1/3c i c oraz d∊ całkowitych (Z₊) (wtedy c=3d) x(x²−d)−9d(x²−d)=0 (x²−d)(x−9d)=0 x²=d lub x=9d x²=d sprzeczne (gdyż d=1/3c, x≠√3/3*c) x=9d czyli x=3c i c∊Z oraz d=1/3c∊Z₊ czyli np. c=3 d=1 spr. W(9d)=0 729d³−9d*81d²−9d²+3d=0 −9d²+3d=0 3d(1−3d)=0 d=0 (sprzeczne) lub d=1/3 (sprzeczne) ? może się pomyliłam w obliczeniach, ale mi tu wychodzi sprzeczność z założeniami, (m.in,) że d jest całkowite

a7: tak pomyłka już od początku, sorry

a7: W(x)=0 gdy np. x³=3cx² i jednocześnie c=dx (wychodzi sprzeczność) W(x)=0 gdy −3cx²=dx i x³=−c c=−x³ (dla x=1 c=−1 i d=3 W(x=1)=0 i spełnione są warunki zadania) W(−1)≠0 (−1 jest drugim możliwym wymiernym pierwiastkiem dla c=−1) to aktualny trop, wrócę do zadania jutro, a może w tzw. międzyczasie ktoś już wykaże to, co zadane.

a7: z wzorów Viete'a dla trójmianu 3 stopnia mamy, że 3c=x₁+x₂+x₃ c=−x₁*x₂*x₃ d=x₁*x₂+x₂*x₃+x₁*x₃ czyli 3c=−3x₁*x₂*x₃ czyli x₁+x₂+x₃=−3x₁*x₂*x₃

	−(x2+x3)
wyliczamy x1=
	1+3x2*x3

aby x₁ było l. wymierną x₂+x₃ musi być liczbą całkowitą i jednocześnie 1+3x₂x₃ musi być liczbą całkowitą (gdyż liczba wymierna to taka której licznik i mianownik to l. całkowite) 1. dla x₂+x₃=0 byłoby x₂=−x₃ i x₁=0 sprzeczne c≠0 2. x₂+x₃ obie są liczbami wymiernymi sumują się do liczby całkowitej

	n		n
i jednocześnie 1+3x2x3 musi być całkowite ⇔ gdy x2=		lub x2=−		i n∊Z
	3x3		3x3

obydwa warunki spełnione jedynie dla ...... czyli...... (?)

a7: * dla wielomianu trzeciego stopnia