Parametr m, funkcja kwadratowa Maturzysta: Dla jakich wartości parametru m nierówność 2x² + 5x + m < 0 ma dokładnie trzy rozwiązania całkowite? Próbowałem Δ≥0, x2=x1+4 (na podstawie interpretacji wykresu przybliżonego) i dalej wzorami Viete'a, ale coś nie chce mi wyjść. Dzięki z góry za pomoc! Odp to m ∊ <−3;0)

Maturzysta: Mam jeszcze jedno: Dla jakich wartości parametru m pierwiastki równania 2x² −(m+3)x + m² −5 = 0 spełniają warunek x1 <1 < x2 I drugie: Dla jakich..... x² + (3m −2)x + m+2 = 0 spełniają x1² +x2² > 1 (tutaj robiłem wstawiając 2x1x2−2x1x2 ale nadal coś mi nie wychodzi? Robię poprawnie?)

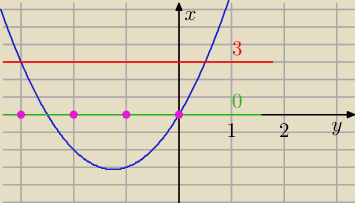
piotr: nierówność 2x² + 5x + m < 0 ma dla: m<0 ilość rozwiązań całkowitych r_c>2 m<−3 ilość rozwiązań całkowitych r_c>3

Maturzysta: @piotr, a czy da się to zrobić jakoś inaczej? Nie do końca rozumiem, o co chodzi tutaj...

ICSP: 2) 2x² − (m+3)x + m² − 5 = 0 1^o Δ > 0 2^o f(1) < 0 3) x² + (3m − 2)x + m + 2 = 0 1^o Δ > 0 2^o x₁² + x₂² = (x₁ + x₂)² − 2x₁x₂ > 1

Maturzysta: Dzięki bardzo, znalazłem błędy rachunkowe, dzięki