liczby zespolone jaros: Obliczyc: (1 + i)⁴ⁿ, n ∊ N Pierwszy raz się z takim czymś spotykam i nie dokona rozumiem o co w tym chodzi, bo nie miałem czegoś takiego na wykładzie

a7: ja się nie znam, ale ja bym zrobiła tak ((1+i)⁴)ⁿ=[(1+i)²(1+i)²]ⁿ=(1+2i+i²)(1+2i+i²)]ⁿ=(2i*2i)ⁿ=(4i²)ⁿ=(−4)ⁿ (?)

Adamm: Przynajmniej jakiś uczuciowy ten spam

a7: i ładny rysunek

jaros: Coś tu się stało? Z tego co wiem to trzeba użyć wzoru Wzór de Moivre'a, ktos by mógł mi to pokazać na tym przykładzie?

ICSP: zacznij od zapisania liczby z = 1 + i w postaci trygonometrycznej.

Mila:

	π
φ=
	4

|1+i|=√2

	π		π
(1+i)4n=(√2)4n*( cos(		*4n)+i sin(		*4n))=
	4		4

=4ⁿ*(cos(π*n)+i sin (π*n))=4ⁿ*cos(π*n) dalej sam W tym zadaniu lepszy jest sposób a7 . (1+i)²=2i

jaros: Dziękuje śliczne za pomoc @Mila, rozumiem twoje kroki lecz nie za bardzo rozumiem co mam zrobić z samym "n". Tutaj ma skorzystać z jakiejś własnosci liczby zespolonej A i jeszcze jak się nie mylę to "isin (π*n))" wyzerowało się przez okres sin = kπ?

jaros: Sposobu @a7 nie rozumiem, nie znam narazie takich przekształceń

Serce w rozterce : x⁴= x²*x² albo np x⁵= x⁴*x= x³*x²= x²*x³= x*x⁴ x⁴ⁿ=( x⁴)ⁿ lub =( xⁿ)⁴ (a+b)²= a²+2ab+b² (1+i)²= 1+2i+i² Poza tym wiesz ze i²=−1 Ma nadzieje ze rozumiesz teraz sposob a7

Jaros: A No tak, teraz rozumiem Dziękuje , lecz nadal nie wiem jak (−4)² otrzymać ze sposobu @Mila, cosπ=−1 lecz w takim przypadku było by (−4)ⁿ*n

Jaros: (−4)ⁿ*

a7: wydaje mi się, że to można zapisać tak cosπn=1 dla n parzystych oraz cosπn=−1 dla n nieparzystych czyli 4ⁿ*cosπn=(−4)ⁿ jednak lepiej, żeby Mila potwierdziła

ICSP: cos(πn) = (−1)ⁿ

jaros: Odp. (−4)ⁿ Wiec mam pytanie jak pozbyć się "n" w cos(π*n) cos(π) = −1 więc gdzie znika to "n" by wynik był taki jak @a7?

a7: już mówię

a7: 4ⁿ*cosπn=4ⁿ*(−1)ⁿ=[4*(−1)]ⁿ=(−4)ⁿ

a7: korzystamy z wzoru aⁿ*bⁿ=(ab)ⁿ

a7: zobacz rysunek Mili z 22:49 cosπn=1 albo cosπn=−1 w zależności czy n jest parzyste czy nieparzyste czyli cosπn=(−1)ⁿ co napisał ICSP

jaros: Jak rozumiem tutaj cosπ*n −−−> w (−1)ⁿ dlaczego tak?

jaros: Tylko to jest jeszcze dla mnie nie jasne

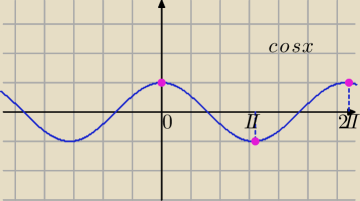
a7: (−1) do potęgi n jest równe 1 gdy n jest parzyste oraz równe −1 gdy n jest nieparzyste, tak samo jak cosπn np. cos0π=cos2π=cos4π=.....=1 a cos1*π=cos3π=cos5π=.....=−1 (zobacz różowe kropki na rysunku Mili z 22:59

jaros: Znaczy chyba nie rozumiemy się do końca, mam na myśli, czy istnieje operacja matematyczna która umożliwia zamiennie iloczynu na potęgowanie, bo tam zachodzi coś takiego

a7: no tak nie rozumiemy się, rzeczywiście, tam chodzi o to co już napisałam najlepiej jak potrafiłam 16:56

jaros: Tylko jeżeli mamy w zdaniu, że n to każda liczba naturalna to np "n = 2" wynik z (−4)ⁿ*n będę miał 32 zamiast 16. Da się to jeszcze jakoś prościej napisać? lub ja popełniłem błąd.

a7: popełniłeś błąd n=2 cos(2π)=1 (−4)ⁿ=16

a7: 4ⁿ*(−1)ⁿ=(−4)ⁿ

a7: n=2 4²*(−1)²=16

a7: nie kumasz chyba tego przejścia cosπn=(−1)ⁿ

a7: cosπn≠n (−1)ⁿ≠n

jaros: Tak tak nie kumam tego! Nie wiem co kompetnie tam się Stalo w jaki sposób iloczyn liczb −1*n przeszedł w formę (−1)ⁿ

jaros: Proszę o pomoc

a7: no bo tam nie ma (−1)*n

a7: tam jest cos(πn)

a7: n należy do naturalnych więc cos(πn)=−1 (dla n nieparzystych) i cos(πn)=1 dla n parzystych czyli cos(πn)=(−1)ⁿ (−1)⁰=1 (−1)²=1 (−1)⁴=1 ........ (−1)¹=−1 (−1)³=−1 (−1)⁵=−1 .......

a7: więc cos(πn)≠1*n

jaros: Aaaaa dobra już rozumiem, DZIĘKUJE!

a7: czy teraz jaśniej, bo jeśli nie to napisz, dokładnie jeszcze raz czego dokładnie, dokładnie nierozumieszi gdzie "nie trybi" to ja (albo ktoś jeszcze)spróbuję jeszcze raz

a7: a spoko

Mila: 1) cos(0π)=1 cos(1π)=−1 cos(2π)=1 cos(3π)=−1 czyli jak piszą wcześniej: cos(nπ)=1 dla n parzystych cos(nπ)=−1 dla n− nieparzystych , co zapisujemy: cos(nπ)=(−1)ⁿ −−−−−−−−−−−−− Zatem: 4ⁿ*cos(nπ)=4ⁿ*(−1)ⁿ=(−4)ⁿ wszystko już zostało napisane wyżej przez A7 i ICSP 2) Czasem warto policzyć na piechotę kwadrat liczby zespolonej i nie korzystać z wzorów de Moivre' a (1+i)²=2i zapamiętaj, często z tego warto skorzystać. (1−i)²=−2i (1+2i)²=−3+4i (1−2i)²=−3−4i (2+i)²=3+4i te wzorki przydają się przy niektórych równaniach kwadratowych.