nierówność Marusia: dana jest nierówność 8<a√2<10 uzasadnij, ze istnieją dokładnie dwie liczby naturalne a, dla których powyższa nierówność jest prawdziwa Jak to obliczyć? Po przekształceniu wyszło mi √32<a<√50

Marusia: bardzo proszę o pomoc

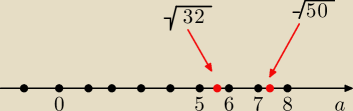
chichi: a∊(4√2,5√2)≈(5.66 , 7.07) zatem dla a∊N istnieją dwie liczby spełniające ową nierówność, te liczby to 6 i 7.

a7: no to widzimy/zauważamy, że nierówność jest spełniona przez dwie liczby naturalne tj. 6 i 7 gdyż √36 i √49 mieszczą si pomiędzy √32 a √50 (inne liczby naturalne już nie spełnią gdyż 8=√64 i to jest większe niż √50 a 5=√25 jest mniejsze niż √32)

a7:

Mila: 8<a√2<10 /² 64<2a²<100 /:2 32<a²<50 a=6 , a=7

Marusia: bardzo dziękuję

Mila: zał. a∊N