jeszcze jedno z geometrii
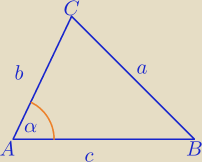
DAniel : Wiedząc, że α,β,γ ą miarami katów wewnętrznych trójkąta leżących naprzeciw boków
| | α | | a | |
o długości odpowiednio a, b, c , dowieść , że: sin |
| ≤ |
| |
| | 2 | | 2√bc | |
4 paź 12:58
Mila:
1) z tw. cosinusów :
a
2=b
2+c
2−2bc cosα
| | b2+c2−a2 | | 1 | | b | | c | | a2 | | 1 | | a2 | |
cosα= |
| = |
| *( |
| + |
| )− |
| ≥ |
| *2− |
| |
| | 2bc | | 2 | | c | | b | | 2bc | | 2 | | 2bc | |
================
4 paź 16:21
Mila:
II sposób z tw. sinusów, spróbuj sam
4 paź 16:21
kerajs: Z tw kosinusów:
a2=b2+c2−2bc cos α
a2=b2+c2−2bc (1−2sin2 α2)
a2−(b−c)2=4bcsin2 α2
dalej sobie poradzisz.
4 paź 16:24
DAniel : Dzięki
4 paź 19:32