Wytłumaczy ktoś jak zrobić takie typu zadanie? Marcin: Dana jest nierówność (m²−1)x−4m+4>0. m∊R , dla jakiego m zbiór rozwiązań tej nierówności zawiera przedział (−∞,0)?

piotr: masz funkcję liniową y = ax + b musi być malejąca ⇒ a < 0 ⇒ m²−1 < 0 ⇒ m ∊ (−1; 1) miejsce zerowe > 0 ⇒ −b/a>0 ⇒(4m−4)/(m²−1) > 0 ⇒ 4m−4<0 ⇒ m < 1 ⇒ m ∊ (−1; 1)

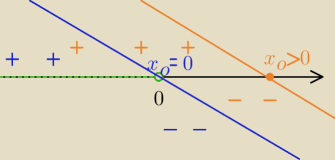
ite: 1/ funkcja musi być malejąca 2/ musi przecinać oś OX w punkcie o odciętej większej lub równej zero

Marcin: a jakbym miał przedział (1,+∞)

Jerzy: Wtedy: m² − 1 > 0 oraz x₀ ≥ 1

Marcin: ok już rozumiem, dzięki

Jerzy: Pomyłka x₀ ≤ 1

ite: Jerzy ale zwrot nierówności (m²−1)x−4m+4>0 pozostaje bez zmian, więc x₀≥1.

ite: moja pomyłka, odpowiedź taka jak pisze Jerzy 11:18 x₀ ≤ 1

Marcin: no tak, bo dzielisz przez ujemną, wtedy zmiana strony nierówności.

Mila: 2) sprawdzamy dla m=−1 0x+4+4=8>0 dla każdego x∊R nierówność jest spełniona f(x) =8− funkcja stała lub m=1 0*x−4+4=0 nierówność nie jest spełniona odp. m∊<−1,1)