pochodna anonim123: Dlaczego tutaj jest taka wskazówka w podpunkcie e) https://zapodaj.net/fa45cc5989b93.jpg.html?

jc: Jak posłuchasz wskazówki, będziesz mógł skrócić Δx i podstawić Δx=0.

anonim123: Ale skąd się bierze wskazówka?

znak:

	√x + Δx − √x
Tam powinno być		.
	Δx

	√x + Δx − √x
To jest taka sztuczka. Bazowo masz		. No, ale taka postać nic nam nie
	Δx

daje. Licząc pochodną z definicji używasz granicy, prawda? Ale cóż Ci da policzenie granicy na dany moment? Nic, symbol nieoznaczony. I tu z pomocą przychodzi kombinowanie, tak jak w granicach. Innymi słowy szukasz wzoru skróconego mnożenia.

√x + Δx − √x		√x + Δx − √x		√x + Δx + √x
	=		*		=
Δx		Δx		√x + Δx + √x

	(√x + Δx)2 − (√x)2		Δx		1
		=		→		,
	Δx(√x + Δx + √x)		Δx(√x + Δx + √x)		2√x

gdy Δx → 0

anonim123:

	1
Nie wychodzi mi ostatnie przekształcenie w wyniku jego ma być		? Sprowadzałam do
	2√x

wspólnego mianownika ale nie uzyskałam poprawnego wyniku.

Jerzy: Skracasz przez Δx,potem podstaywiasz Δx = 0

znak: Tak, ma wyjść dokładnie tak. Jakie konkretnie przekształcenie Ci nie wychodzi? Przejście do

	1
granicy? Najpierw skracasz licznik i mianownik, a wtedy otrzymujesz		.
	√x + Δx + √x

	1		1
Wówczas		→		, gdy Δx → 0
	√x + Δx + √x		2√x

Albo tak jak jc napisał, podstawiasz w miejsce Δx zero − możesz tak zrobić, bo nie prowadzi to do nieporozumienia − i dostajesz to samo.

anonim123: To dodawałam √x + Δx + √x i źle mi wyszło.

anonim123: Jeszcze jednego nie rozumiem w jaki sposób została znaleziona wartość funkcji z(t+delta t) Całości tego znajdywania nie rozumiem. https://zapodaj.net/5ff1348d20f54.jpg.html

Qulka: zrób sobie z definicji pochodnej

	f(x+Δx)−f(x)
f' ≈
	Δx

więc f' •Δx ≈f(x+Δx)−f(x) f' •Δx +f(x)≈f(x+Δx)

anonim123: A w udostępnionym linku liczą z definicji pochodnej? Jak liczą w podanym przykładzie?

Qulka: tak jakby , bo zrobili to strasznie zawile

anonim123: Może ktoś opisać rozumowanie jakim się kierowano przy obliczaniu przybliżonej wartości funkcji w linku sposób Qulki rozumiem

Qulka: za godzinę

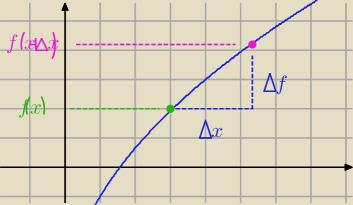
Qulka: w matematyce najczęściej zmienną jest x w fizyce t więc zróbmy na x

	Δf		Δf
wzór 4.1 to f' = lim		≈		więc mnożąc przez mianownik Δf ≈ f'•Δx
	Δx		Δx

f(x+Δx) = f(x)+Δf (patrz rysunek) (lub http://matematykadlastudenta.pl/strona/15.html) podstawiając wzór 4.1 zamiast Δf f(x)+Δf ≈ f(x)+f'•Δx co daje wzór 4.2

anonim123: Dziękuję

anonim123: link który podałaś nie działa

ICSP: usuń z niego nawias na końcu a zadziała

Qulka: http://matematykadlastudenta.pl/strona/15.html

anonim123: Dzięki