Planimetria - dowody Ilona: W trójkącie równobocznym ABC na bokach AB i BC wybrano odpowiednio punkty P i Q tak, że |AP|=2|BP| i |CQ|=2|BQ|. Odcinki AQ i CP przecinają się w punkcie S.Uzasadnij, że trójkąty APS i CQS są przystające. Na pierwszy rzut oka widać, że AP=CQ i kąt ASP= kąt CSQ. Nie wiem jakimi zapisami udowodnić resztę brakujących cech przystawania trójkątów APS i CQS.

Qulka: zacznij że ABQ≡CBP będziesz miała pozostałe kąty

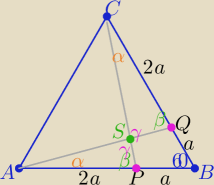
Eta: 1/ ΔABQ≡ΔBPC z cechy (bkb) 2/ ΔAPS≡ΔCQS z cechy ( kbk)

Mila: Hej

Eta: Hejjjjjjj