Pola trapezu endrju: W trapezie ABCD, ABIICD, przekątne przecinają się w punkcie E. Wiedząc że pola trójkątów ABE i CDE są odpowiednio równe 90cm² i 40cm², oblicz pole trójkąta AED.

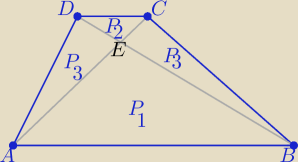
Eta: P₃=√P₁*P₂ P(AED)=P₃= 60

Minato:

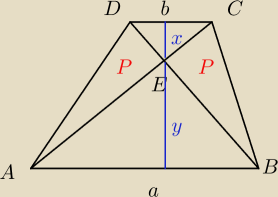
	90		3
ΔABE ~ ΔCDE w skali k2 =		→ k =		(cecha kkk)
	40		2

	3
a =		b
	2

	3
y =		x
	2

	1		1		5		5		25
Ptrapezu =		(a+b)(x+y) =		*		b*		x =		bx
	2		2		2		2		8

	1
PCDE =		bx = 40
	2

	25
Ptrapezu =		*80 = 250
	8

250 = 2P + 90 + 40, warto pokazać, że pola trójkątów AED i BEC są równe P = 60 cm²

Eta:

Eta: P(trapezu)= (√P₁+√P₂)² i P₃=P₄=√P₁*P₂ P= (5√10)² P=250

Minato: Eta jak zwykle rzuci wzorkami

Eta: Można też takimi:

	P1		3
skala podobieństwa Δ ABE i CDE : k2=		⇒ k=
	P2		2

P₃=P₄= k*P₂ i P=(k+1)²*P₂

	3
P3=P4=		*40 = 60
	2

	25
P=		*40 = 250
	4