optymalizacja
pomocyy:
*to znowu ja*
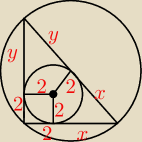
Na kole o promieniu 2 opisano trójkąt prostokątny. Wyznacz wymiary trójkąta, dla którego
promień koła na nim opisanego jest najmniejszy.
x+y = 2R
(x+2)
2 + (y+2)
2 = (x+y)
2
x
2 + 4x + 4 + y
2 + 4y + 4 = x
2 + 2xy + y
2
4x + 4y + 8 = 2xy
4x − 2xy = −4y − 8
2x(2 − y) = −4(y + 2) |: 2(2 − y)
x =
−4(y + 2)2(2 − y)
x =
−2(y + 2)(2 − y)
x =
−2(y + 2)−1(y − 2)
x =
2(y + 2)(y − 2)
x =
2y + 4(y − 2)
Dobrze do tego momentu? Jeśli tak to co dalej? Bo nie mam pojęcia
16 wrz 19:13
wredulus_pospolitus:
no dobrze
i teraz wstawiasz do funkcji
f(x,y) = x+y 'za x' i otrzymujesz funkcje jednej zmiennej której szukasz minimum w
przedziale (2, +∞)
16 wrz 19:16
wredulus_pospolitus:
w sensie ... y ∊ (2,+∞)
16 wrz 19:17
wredulus_pospolitus:
PS. używaj U zamiast u do zapisu ułamków:
16 wrz 19:18
pomocyy: Skąd się bierze wzór tej funkcji? Jest to przeciwprostokątna?
16 wrz 19:18
wredulus_pospolitus:
c = x+y = 2R <−−− stąd

16 wrz 19:18
wredulus_pospolitus:
chcesz znaleźć najmniejszy R ... więc chcesz znaleźć najmniejszą wartość funkcji f(x,y) =
| | x+y | |
|
| lub jak wolisz g(x,y) = x+y |
| | 2 | |
16 wrz 19:19
pomocyy: | | 2y + 4 | | y(y − 2) | |
f(y) = |
| + |
| |
| | y − 2 | | y − 2 | |
| | 2y + 4 + y2 − 2y | |
f(y) = |
| |
| | y − 2 | |
Chyba już nic więcej nie zrobię z tym. Mam teraz liczyć pochodną tego co mi wyszło?
16 wrz 19:27
wredulus_pospolitus:
dokładnie
16 wrz 19:28
pomocyy:
I co mam teraz zrobić?
16 wrz 19:33
pomocyy: 2y = 0?
16 wrz 19:33
Blee:
Co... Bzdura

Sprawdź wzór na pochodną ilorazu

16 wrz 19:33
pomocyy: | | 2y(y − 2) − (4 +y2)1 | |
f '(y) = |
| |
| | (y − 2)2 | |
| | 2y2 − 4y − 4 − y2 | |
f '(y) = |
| |
| | (y − 2)2 | |
| | y2 − 4y − 4 | |
f '(y) = |
| |
| | (y − 2)2 | |
Dobrze teraz? Jak tak to teraz mam zrobić to?
16 wrz 19:44
pomocyy: Dobra zrobiłem. Dzięki obojgu za pomoc i za radę co do pisania tutaj. Miłego wieczorku
16 wrz 19:50
wredulus_pospolitus:
Miluś ... a czemu (bez wykazania) przyjmujesz że a = b

Na jakiej podstawie to czynisz

16 wrz 21:00
Mila:
Dlatego poszłam na skróty, bo nie przeczytałam dokładnie treści

Pozdrawiam

16 wrz 21:28
Mila:
1)
(x+2)
2+(y+2)
2=(x+y)
2
⇔
y=U{2x+4}{x−2), x≠2
f
min dla x=2+2
√2
wtedy:
| | 2*(2+2√2)+4 | | 4+4√2+4 | |
y= |
| = |
| =2+2√2⇔ |
| | 2+2√2−2 | | 2√2 | |
x=y
c=4+4
√2
R=2+2
√2
3) a=4+2
√2
b=4+2
√2
a=b
=============
16 wrz 22:17
 *to znowu ja*
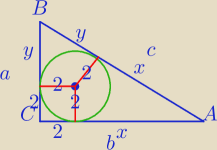
Na kole o promieniu 2 opisano trójkąt prostokątny. Wyznacz wymiary trójkąta, dla którego
promień koła na nim opisanego jest najmniejszy.
x+y = 2R
(x+2)2 + (y+2)2 = (x+y)2
x2 + 4x + 4 + y2 + 4y + 4 = x2 + 2xy + y2
4x + 4y + 8 = 2xy
4x − 2xy = −4y − 8
2x(2 − y) = −4(y + 2) |: 2(2 − y)
x = −4(y + 2)2(2 − y)
x = −2(y + 2)(2 − y)
x = −2(y + 2)−1(y − 2)
x = 2(y + 2)(y − 2)
x = 2y + 4(y − 2)
Dobrze do tego momentu? Jeśli tak to co dalej? Bo nie mam pojęcia
*to znowu ja*
Na kole o promieniu 2 opisano trójkąt prostokątny. Wyznacz wymiary trójkąta, dla którego
promień koła na nim opisanego jest najmniejszy.
x+y = 2R
(x+2)2 + (y+2)2 = (x+y)2
x2 + 4x + 4 + y2 + 4y + 4 = x2 + 2xy + y2
4x + 4y + 8 = 2xy
4x − 2xy = −4y − 8
2x(2 − y) = −4(y + 2) |: 2(2 − y)
x = −4(y + 2)2(2 − y)
x = −2(y + 2)(2 − y)
x = −2(y + 2)−1(y − 2)
x = 2(y + 2)(y − 2)
x = 2y + 4(y − 2)
Dobrze do tego momentu? Jeśli tak to co dalej? Bo nie mam pojęcia

 Sprawdź wzór na pochodną ilorazu
Sprawdź wzór na pochodną ilorazu
 Na jakiej podstawie to czynisz
Na jakiej podstawie to czynisz 
 Pozdrawiam
Pozdrawiam
 1)
(x+2)2+(y+2)2=(x+y)2
⇔
y=U{2x+4}{x−2), x≠2
1)
(x+2)2+(y+2)2=(x+y)2
⇔
y=U{2x+4}{x−2), x≠2