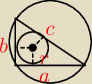
 Na kole o promieniu 2 opisano trójkąt prostokątny. Wyznacz wymiary trójkąta, dla którego
promień koła na nim opisanego jest najmniejszy.
Dane:
r = 2
c = y+x
b = 2 + y
a = 2 + x
R = x+y2
zał: x,y>0 oraz x=y
stąd x=y, ponieważ w zadaniu mamy: WYZNACZ WYMIARY TRÓJKĄTA, dla którego promień koła na nim
opisanego jest NAJMNIEJSZY.
Rozumiem to tak, że skoro promień ma być najmniejszy, to będzie tylko i wyłącznie wtedy jak c
będzie najmniejsze.
Żeby c było najmniejsze x i y musi być równy bo: 2+1 uznajmy że x i y są równe 1 to 3.
Gdyby były różne to nie nie będzie to najmniejsza opcja (np. x=1 y=2 to mamy 3 i 4 −> 4>3 (3 z
poprzedniej linijki)
Mógłby mi ktoś wytłumaczyć dlaczego takie założenie jest złe i jak zrobić to zadanie poprawnie?
Dziękuje.
Na kole o promieniu 2 opisano trójkąt prostokątny. Wyznacz wymiary trójkąta, dla którego
promień koła na nim opisanego jest najmniejszy.
Dane:
r = 2
c = y+x
b = 2 + y
a = 2 + x
R = x+y2
zał: x,y>0 oraz x=y
stąd x=y, ponieważ w zadaniu mamy: WYZNACZ WYMIARY TRÓJKĄTA, dla którego promień koła na nim
opisanego jest NAJMNIEJSZY.
Rozumiem to tak, że skoro promień ma być najmniejszy, to będzie tylko i wyłącznie wtedy jak c
będzie najmniejsze.
Żeby c było najmniejsze x i y musi być równy bo: 2+1 uznajmy że x i y są równe 1 to 3.
Gdyby były różne to nie nie będzie to najmniejsza opcja (np. x=1 y=2 to mamy 3 i 4 −> 4>3 (3 z
poprzedniej linijki)
Mógłby mi ktoś wytłumaczyć dlaczego takie założenie jest złe i jak zrobić to zadanie poprawnie?
Dziękuje.
 Na jakiej podstawie dochodzisz do wniosków przed
rozwiązaniem zadania
Na jakiej podstawie dochodzisz do wniosków przed
rozwiązaniem zadania  Ty musisz pokazać dlaczego ma zachodzić x=y (na tym właśnie polega to zadanie). Ty tego nie
pokazałeś tylko od razu założyłeś, ze tak będzie 'bo tak'.
Ty musisz pokazać dlaczego ma zachodzić x=y (na tym właśnie polega to zadanie). Ty tego nie
pokazałeś tylko od razu założyłeś, ze tak będzie 'bo tak'.

| 2y + 4 | ||
x = | ||
| 2y − 2 |
| 2y + 4 | ||
f(x,y) = x+y −−> f(y) = | + y i szukasz minimum tejże funkcji | |
| 2y − 2 |