Skąd wiadomo, że dany kąt jest prosty?
Egon:
Zadanie: Oblicz objętość ostrosłupa prawidłowego czworokątnego mając długość krawędzi podstawy
a i miarę 2α kąta między dwiema sąsiednimi ścianami bocznymi.
Tak właściwie rozwiązanie tego zadania jest dość łatwe do znalezienia w internecie. Moim
problemem jest fakt, że nie rozumiem fragmentu tego rozwiązania. Bardzo proszę o oświecenie
mnie.
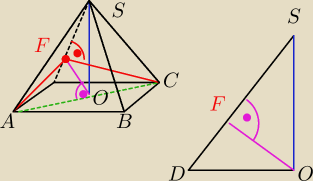
Mamy sobie ostrosłup ABCDS (wierzchołka D nie podpisałem, bo taki genialny ze mnie rysownik, że
w sumie nie bardzo zostawiłem sobie na to miejsce xD). Czerwone linie są prostopadłe do
odcinka DS. Pomiędzy nimi jest kąt 2α. Różowa linia to wysokość trójkąta równoramiennego ACF.
Dzieli ona kąt α na pół. Siłą rzeczy jest prostopadła do odcinka AC. Dotąd jeszcze rozumiem XD
Jednak w dalszej części rozwiązania, które znalazłem, bierzemy sobie trójkąt DOS, gdzie nasz
różowy odcinek FO, będący wysokością trójkąta ACF, jest jednocześnie wysokością trójkąta DOS i
jest prostopadły do odcinka DS. Moje pytanie brzmi − skąd powinienem wiedzieć, że tak jest?
Skąd wiadomo, że odcinek FO jest prostopadły do odcinka DS?
wredulus_pospolitus:
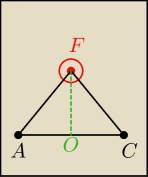
Tok rozumowania:
1) kąt pomiędzy ścianami to kąt pomiędzy wysokościami AF i CF
2) związku z tym zarówno AF jak i CF są prostopadłe do DS
3) AF i CF tworzą nam trójkąt ACF
4) wszystkie odcinki zawarte w tym trójkącie będą prostopadłe do DS, w szczególności OF
Najłatwiej by było Ci to zauważ, jeżeli weźmiesz sobie kartkę papieru i wbijesz w niego ołówek.
Narysuj sobie trójkąt na kartce.
Ołówek jest Twoją krawędzią DS a punkt przebicia przez kartkę to punkt F.
Jak widzisz FO będzie prostopadła do ołówka (czyli Twojego DS) tak samo zresztą jak każdy inny
odcinek poprowadzony z F do dowolnego miejsca na AC.
wredulus_pospolitus:
Mam nadzieję, że jak zrobisz to, to zrozumiesz, że faktycznie tak to jest
