F. kwadratowa Popa: Cześć. Nie mogę za nic rozwiązać algebraicznie zadania: Dla jakich m x|x−2|= m+1 ma 2 różne rozw. Próbowałem rozbijać na przypadki i korzystać ze wzorow viete'a ale nie wychodzi. Proszę o pomoc.

ICSP: Dla x ≥ 2 (x−1)² = m + 2 Jeśli tylko m ≥ −1 to z powyższego równania dostaniemy jedno rozwiązanie. W przeciwnym wypadku brak rozwiązań Dla x < 2 (x−1)² = −m Jeżeli m > 0 to rozwiązań nie ma. Jeżeli m = 0 mamy jedno rozwiązanie Jeżeli m < −1 mamy jedno rozwiązanie Dla m = −1 mamy jedno rozwiązanie Dla m ∊ (−1 ; 0) dwa rozwiązania Ostatecznie zatem m = −1 lub m = 0

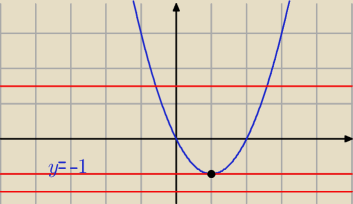
gamma: y = x² − 2x y = m + 1 (wykres funkcji stałej) dla m + 1 < −1 ⇒ m < −2 brak rozwiązań dla m + 1 = −1 ⇒ m = −2 jest jedno rozwiązanie dla m + 1 > −1 ⇒ m > −2 są dwa rozwiązania ........................................................................................ algebraicznie: x² − 2x − (m + 1) = 0 2 rózne rozwiązania dla Δ > 0 ⇒ 4 + 4m + 4 > 0 ⇒ m > −2

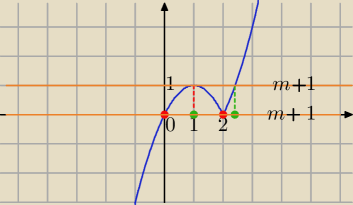
Mila: Graficznie: f(x)=x*|x−2| dwa rozwiązania dla m+1=0 lub m+1=1 m=−1 dwa rozwiązania x=0 lub x=2 m+1=1 ⇔m=0 dwa rozwiązania : x=1 lub x²−2x=1 x=1+√2 m∊{−1,0}