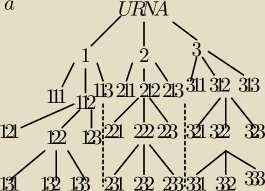
Reguła mnożenia xyz: Możecie sprawdzić czy dobrze, a jak da się lepiej to podpowiecie? Treść zadania: W urnie znajdują się trzy kule oznaczone numerami: 1, 2, 3. Trzykrotnie wyciągamy kulę, zapisujemy jej numer i zwracamy ją do urny. Zapisane numery tworzą liczbę trzycyfrową. a) Narysuj drzewko, tak aby ilustrowało wszystkie możliwe wyniki tego doświadczenia. b) Ile w ten sposób możemy otrzymać liczb parzystych? Odp: 9: 112, 222, 332, 122, 213, 322, 132, 232, 312 c) Ile w ten sposób możemy otrzymać licz podzielnych przez 6? Odp: 3: 222,132, 312 (wykorzystałem cechę podzielności przez 6)

xyz: Zadanie 2 a) Uzasadnij, że liczb trzycyfrowych podzielnych przez 5 jest mniej niż 200: 100, 105, 110, ..., 990, 995 995 = 100 + (n−1)5 995 = 100 + 5n − 5 995 = 5n + 95 5n = 900 l:5 n = 180 180 < 200 cnd. b) Uzasadnij, że jest ponad 2000 liczb pięciocyfrowych podzielnych przez 5, w których mogą występować cyfry: 0, 1, 2, 3, 4, 5. 1 cyfra: [1,2,3,4,5] −> 5 2 cyfra: [0,1,2,3,4,5] −> 6 3 cyfra: [0,1,2,3,4,5] −> 6 4 cyfra: [0,1,2,3,4,5] −> 6 5 cyfra: [0,5] −> 2 5*6³*2 = 2160 2160 > 2000 cnd.

xyz: Jeszcze to zadanie 2 prosiłbym

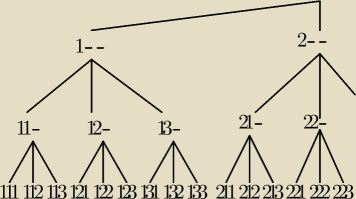
wredulus_pospolitus: Wiem, że drzewo duże i dlatego nie mogłeś/−aś go dobrze przerysować. Tutaj masz połowę drzewa. Tak go masz?

wredulus_pospolitus: Cała reszta −−− 'spoko'