trójkąt
Michał:
Dany jest trójkąt równoboczny ABC wewnątrz którego zaznaczono punkt P
tak,że zachodzi równość m2+n2=k2
gdzie m,n,k są odległościami punktu P odpowiednio od wierzchołków A,B,C
Oblicz miarę kata APB i długość boku trójkąta ABC
9 wrz 20:40
Eta:
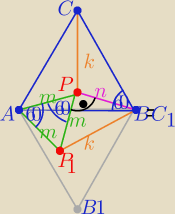
Po obrocie wokół punktu A o kąt 60
o ( patrz rys)
to otrzymujemy ΔAPP
1 −− równoboczny o boku m
oraz ΔPP
1C
1 −− prostokątny bo m
2+n
2=k
2 ( z treści zad.)
więc |∡APB|=60
o+90
o= 150
o
=====================
i z tw. cosinusów w ΔAPB:
|AB|
2=m
2+n
2−2mn*cos150
o
......................
|AB|=
√m2+n2+mn√3
===================
9 wrz 22:26
Mila:
Zgadza się. Też zrobiłam obrót (w drugą stronę).
Pozdrawiam

10 wrz 14:50
kerajs: Elegancki, lecz trikowy sposób.
Przechodząc na geometrię analityczną łatwo wykazać że P leży na krótszym łuku AB okręgu o
środku w B1 i promieniu AB.
Ten kąt wpisany jest oparty na tym samym łuku co kąt środkowy o mierze 360−60 stopni, więc ma
on 150 stopni.
10 wrz 18:00
Mila:
Problem w tym, że ostatnio umieszczamy rozwiązania i autor nie nie interesuje się rozwiązaniem.
10 wrz 18:34
Eta:
Wysilamy się

i.............................
też pozdrawiam

10 wrz 20:42
a7: no właśnie ja tego nie rozumiem, chyba trzeba zacząć to komunikować autorom wątków, może przy
każdym rozwiązaniu powinna być możliwość polubienia albo kliknięcia w dziękuję i ilość
wyświetleń?
10 wrz 20:50
znak: To całkiem dobry pomysł.
10 wrz 21:09
a7: zgłosiłam ten pomysł do Jakuba chociaż nie wiem czy jest/byłaby w ogóle taka możliwość
"programistyczna" w przypadku tego forum
10 wrz 21:29
kerajs: Przypuszczam, że autor tematu jest zainteresowany, lecz wyłącznie do momentu uzyskania pełnego
rozwiązania na którymś z kilku forów na które wrzucił problem (lub foty rozwiązania od kumpla
który ma dobrego korepetytora).
Pewnie uważają, że rozwiązanie należy się im jak psu kiełbasa.
A co do zmian, to sugerowałbym sensowniejszy edytor wzorów matematycznych.
11 wrz 09:14
 Po obrocie wokół punktu A o kąt 60o ( patrz rys)
to otrzymujemy ΔAPP1 −− równoboczny o boku m
oraz ΔPP1C1 −− prostokątny bo m2+n2=k2 ( z treści zad.)
więc |∡APB|=60o+90o= 150o
=====================
i z tw. cosinusów w ΔAPB:
|AB|2=m2+n2−2mn*cos150o
......................
|AB|= √m2+n2+mn√3
===================
Po obrocie wokół punktu A o kąt 60o ( patrz rys)
to otrzymujemy ΔAPP1 −− równoboczny o boku m
oraz ΔPP1C1 −− prostokątny bo m2+n2=k2 ( z treści zad.)
więc |∡APB|=60o+90o= 150o
=====================
i z tw. cosinusów w ΔAPB:
|AB|2=m2+n2−2mn*cos150o
......................
|AB|= √m2+n2+mn√3
===================

 i.............................
też pozdrawiam
i.............................
też pozdrawiam 