nierówność xxx: Wykaż,że dla dowolnych dodatnich liczb rzeczywistych a,b,c zachodzi nierówność √a+b+√a+c+√b+c≥√2(√a+√b+√c)

ICSP: Dla ładniejszego zapisu pomijam na początku pierwiastek.

	1		1
a + b =		(2a + 2b) =		(a + 2√ab + b + a − 2√ab + b) =
	2		2

	(√a − √b)2 + (√a + √b)2		(√a + √b)2
=		≥
	2		2

Dlatego(f(x) = √x jest funkcją monotoniczną) :

	1
√a + b ≥		(√a + √b)
	√2

analogicznie:

	1
√a + c ≥		(√a + √c)
	√2

	1
√c + b ≥		(√c + √b)
	√2

Dodanie ostatnich trzech nierówności stronami daje tezę. Równość gdy √a = √b = √c ⇒ a = b = c

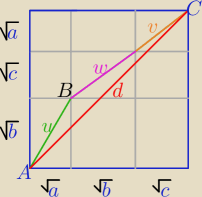a@b: Można też tak ( geometrycznie) z Pitagorasa u=√a+b , w=√b+c, v=√a+c i d= (√a+√b+√c)*√2 i z nierówności trójkąta ABC u+w+v≥d i mamy tezę: √a+b+√a+c+√b+c≥√2(√a+√b+√c) =============================