Kolejność wykonywania przekształceń funkcji, zadanie i problem Aneta: Dzień dobry, mam pewien problem z przekształceniami funkcji. Treść zadania: Na rysunku obok przedstawiony jest wykres funkcji f. Wykonując odpowiednie przekształcenia, naszkicuj wykres,

	1
c) y =		f(|x| + 2)
	2

	1
No, więc zaczęłam przekształcać funkcje f(x) do		f(|x| + 2)
	2

	1		1		1
f(x) →		f(x) (powinowactwo wzgledem osi x, skala		) →		f(|x|) (cześciowa
	2		2		2

	1
symetria wzgledem Oy) →		f(|x| + 2) (translacja o wektor [−2, 0]
	2

teoretycznie wszystko ok, bo otrzymałam tę funkcję o która prosili, lecz po narysowaniu po kolei tych przekształceń otrzymuję coś zupełnie innego niż w odpowiedziach. żeby otrzymac to o co proszą musiałabym najpierw wykonac translację potem symetrię a na koniec powinowactwo. Moje pytanie: czy jest jakaś ustalona kolejność wykonywania przekształceń funkcji? (np. że powinowactwo zawsze pod koniec wykonujemy) Bardzo proszę o pomoc, niedługo będę miała sprawdzian

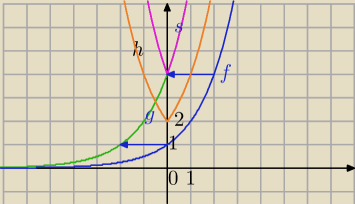
Mila: Dany wykres funkcji f(x) 1) →T_[0,−2]⇒ otrzymujesz wykres funkcji g(x)=f(x+2) 2)f(x+2)→S_OY tej części wykresu która leży z prawej strony OY⇒s(x)=f(|x|+2) 3) Powinowactwo ⇒otrzymujesz wykres funkcji: h(x)=(1/2)*f(|x|+2) Spróbuj teraz swój wykres tak przekształcić i napisz , czy zgadza się z odpowiedzią.

Mila: Poprawka zapisu. 1) Translacja o wektor [−2,0]

ABC: Kolejność jest ważna, czasami jest taka sytuacja że nie gra roli, ale lepiej zawsze ją zachowywać

Mila: Zaczynaj od środka.

Aneta: Co to znaczy żeby zaczynać od srodka?

Mila: Masz dany wykres funkcji f(x); Pierwsze przekształcenie takie, aby otrzymać wykres funkcji y=f(x+2), Potem y=f(|x|+2) ...