Prosta równoległa do boku Ab trójkąta ABC przecięła bok AC w punkcie P i bok BC nika1: Prosta równoległa do boku Ab trójkąta ABC przecięła bok AC w punkcie P i bok BC w punkcie Q. Oblicz stosunek ^|CP|_|AP| , wiedząc że pole trójkąta PCQ jest 3 razy większe od pola trapezu ABQP.

Qulka: figury podobne

Pg		3
	=
Pc		4

CP		√3
	=
PA		2

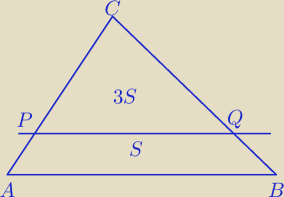
Mila: 1)ΔCPQ∼ΔABC w skali k

PΔCPQ		3S		3
	=k2=		=
PΔABC		4S		4

	√3
k=
	2

2)

CP		√3		√3
	=		⇔ |CP|=		*|AC|
AC		2		2

	√3		√3		2−√3
|AP|=|AC|−|CP|=|AC|−		*|AC|=|AC|*(1−		)=|AC|*
	2		2		2

3)

CP		√3   *|AC| 2
	=		⇔
AP		2−√3   |AC|*   2

CP
	=2√3+3
AP

===============

Qulka: faktycznie trochę za szybko chciałam