pole trójkąta
marco:
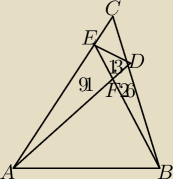
pola na rysunku : 91,13,26
Oblicz pole ABC
4 wrz 19:30
kasia: jedyne dane jakie masz? nie ma kątów podanych
4 wrz 19:43
a@b:
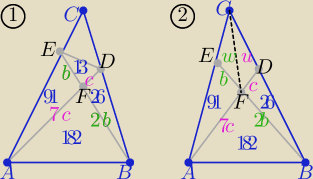
Na rys. 1 ΔAFE i Δ DFE mają wspólną wysokość
| | 91 | |
to ich podstawy są w stosunku |
| =7 |
| | 13 | |
zatem |AF|=7c i |FD|=c
analogicznie ΔBED i EFD
to |BF|=2b i |EF|=b
zatem P(ABF)=2*91= 182
Na rys. 2
w ΔADC : 7*u=91+w oraz w ΔBEC : 2*w=26+u
rozwiązując ten układ równań otrzymasz
u=16 i
w= 21
to P(ABC)= 182+91+26+u+w
P(ABC)=336
4 wrz 20:50
Mila:
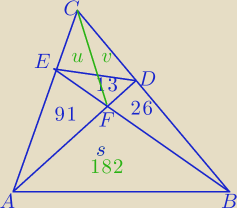
1)
s=7*26=182
2) [EFC]=u, [DFC]=v
| | v | | v+u+91 | | v | | v+u+91 | |
a) |
| = |
| ⇔ |
| = |
| |
| | 26 | | 182+26 | | 26 | | 208 | |
8v=v+u+91⇔
7v−u=91
b)
| u | | u+v+26 | | u | | u+v+26 | |
| = |
| ⇔ |
| = |
| |
| 91 | | 91+182 | | 91 | | 273 | |
3u=u+v+26
2u−v=26 i
7v−u=91
u=21 i v=16
3) P
ABC=182+91+26+16+21=336
Tak jak wyżej

4 wrz 22:56
 pola na rysunku : 91,13,26
Oblicz pole ABC
pola na rysunku : 91,13,26
Oblicz pole ABC
 Na rys. 1 ΔAFE i Δ DFE mają wspólną wysokość
Na rys. 1 ΔAFE i Δ DFE mają wspólną wysokość
 1)
1)
