trójkąt trójkąt: Punkt D jest środkiem boku AB trójkąta równobocznego ABC Na bokach AC i BC zaznaczono odpowiednio punkty E i F tak że kąt EDF=60^o Wykaż że zachodzi równość |AE|+|BF|=|EF|+0,5|AB|

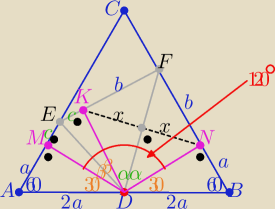
Eta: |AB|=4a to |AM|=|BN|=2a i |MD|=|NB|=a√3 punkt K jest symetryczny do punktu N względem prostej FD to |KD|=|MD|=|NB|=a√3 |∡MDN|=120^o= 2α+2β , bo α+β=60^o z treści zadania zatem ΔFND ≡ΔFKD z cechy (bkb) to |FN|=|KF|=b punkt K ∊EF bo |∡FKD|+|∡EKD|=180^o więc ΔEMD≡ΔEKD to |ME|=|EK|=c i mamy tezę:

	1
|AE|+|BF|=a+c+a+b= c+b+2a = |EF|+		|AB|
	2

===================================