trójkąt tomx: W trójkącie ABC kąt przy wierzchołku B ma miarę dwa razy mniejszą od miary kąta przy wierzchołku C Wykaż,ze |AB|²=|AC|(|AC|+|BC|)

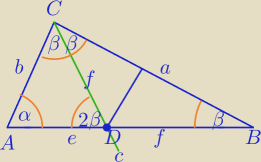
Mila: 1) z tw. o dwusiecznej :

b		e
	=		i e+f=c⇔f=c−e
a		f

2) Z podobieństwa trójkątów ΔADC∼ΔABC

b		c
	=		⇔b2=c*e
e		b

	b2
e=
	c

3) z (1) i (2)

b		b2   c
	=
a		b2   c−   c

b		b2		1		b
	=		⇔		=
a		c2−b2		a		c2−b2

c²−b²=ab ⇔c²=ab+b²⇔ |AB|²=⇔|AC|*(|BC|+|AC|) cnw ============

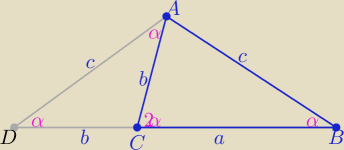
Eta: To ja "tradycyjnie" z podobieństwa trójkątów ADB i ACD z cechy (kkk)

c		b
	=
a+b		c

c²=b(b+a) |AB|²=|AC|(|AC|+|BC|) ================= c.n.w.