trójkąt janko: W okrąg o środku S wpisano trójkąt równoboczny ABC w którym punkt D jest środkiem boku AC Na krótszym łuku AB zaznaczono punkt P Wiedząc, że punkt M jest punktem symetrycznym do punktu P względem punktu D Wykaż ze |MP|=|MB|

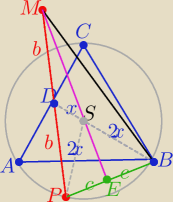
Eta: 1/ rysunek E −− środek odcinka PB BD −− środkowa ΔABC i ΔPBM to |DS|=x i |BS|=2x punkt S jest środkiem ciężkości ΔABC i ΔPBM więc punkty S , E i M leżą na jednej prostej EM, która jest jednocześnie symetralną podstawy AB w ΔPBM a zatem ΔPBM jest równoramienny i mamy tezę: |PM|=|BM| =========