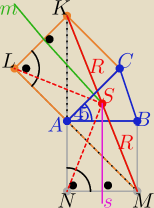
 1/rysunek zgodny z treścią
Zauważ,że punkty A,N,K oraz punkty A,M,L, leżą na jednej prostej
( bo ∡KAN=180o oraz ∡LAM=180o
Na trójkątach NMK i KLM można opisać okrąg o średnicy|MK|=2R
którego środek jest w punkcie S
zatem symetralne s i m boków NM i KL pokrywają się
z symetralnymi boków AB i AC i przecinają się w punkcie S
i mamy tezę :
S jest środkiem odcinka MK i środkiem okręgu opisanego na trójkącie ABC
=========================================================
1/rysunek zgodny z treścią
Zauważ,że punkty A,N,K oraz punkty A,M,L, leżą na jednej prostej
( bo ∡KAN=180o oraz ∡LAM=180o
Na trójkątach NMK i KLM można opisać okrąg o średnicy|MK|=2R
którego środek jest w punkcie S
zatem symetralne s i m boków NM i KL pokrywają się
z symetralnymi boków AB i AC i przecinają się w punkcie S
i mamy tezę :
S jest środkiem odcinka MK i środkiem okręgu opisanego na trójkącie ABC
=========================================================