czworokąt megas: W czworokącie wypukłym ABCD w którym |AD|=m , |BC|=n i suma kątów przy boku AB jest równa 90^o oraz punkt E jest środkiem boku DC Wyznacz wartość wyrażenia P_ABE−P_ADE−P_BCE

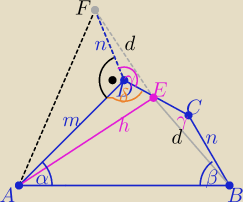
Eta: 1/ rysunek punkty B i F symetryczne względem punktu E to z cechy (bkb) ΔBCE ≡ΔDEF więc mają równe pola i |DF|=|BC|=n oraz ΔABE i AFE też mają równe pola ( bo mają wspólną wysokość poprowadzoną na równej długości podstawy BE i EF w czworokącie ABCD α+β+γ+δ= 360^o ⇒ zatem ∡ADF|= 360^o −(γ+δ) = α+β= 90^o

	mn
więc P(ΔADF)=
	2

zatem

	mn
W=P(AFE)−P(ADE)−P(EDF)= P(ADF)=
	2

	mn
W=
	2

===========