kat jun: Wewnątrz równoległoboku ABCD rozważmy punkt P taki ze ∠ ADP =∠ABP oraz ∠ DCP = 30^o . Oblicz miarę kata DAP.

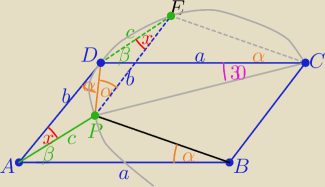
Eta: Budujemy równoległobok APED o bokach b i c kąty naprzemianległe α i kąty ostre x wtedy ΔABP≡ΔDCE z cechy ( bkb) więc |∡ABP|= |∡DCE|=α= |∡DPE| to na czworokącie DPCE da się opisać okrąg Kąty wpisane oparte na łuku DP mają równe miary zatem |∡BCP|=30^o=|∡DEP|=x= |∡DAP| |∡DAP|=30^o =========

Eta: Poprawiam chochlika oczywiście ma być zatem |∡DCP|=30^o=......

jaan: W trójkącie ABC punkt D jest środkiem odcinka AB Wiedząc,że |<BAC|+|<BCD|=90^o Wykaż,że trójkąt ABC jest prostokątny lub równoramienny

Eta: Załóż nowy post !

jaan: OK

Eta: A tak z grzeczności, ładnie by było podziękować za rozwiązanie ( a nie tylko wrzucać nowe zadania)