pole UP: Oblicz pole trójkąta o bokach długości √5,√13, √26

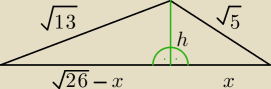
getin: { h² + x² = (√5)² { (√26−x)² + h² = (√13)² { h² + x² = 5 { 26 − 2√26*x + x² + h² = 13 26 − 2√26*x + 5 = 13

	18		9
x =		=
	2√26		√26

	9
h2 + (		)2 = 5
	√26

	81
h2 +		= 5
	26

	49
h2 =
	26

	7
h =
	√26

	1		1		7		7
P =		a*h =		*√26*		=
	2		2		√26		2

Można też to obliczyć wzorem Herona wtedy będzie bez rysunku i Pitagorasa

ula: Wzór Herona.

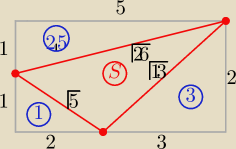
Eta: P▭=10 S=10 −(1+3+2,5) S=3,5 =======

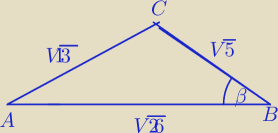
Mila: III sposób β− kąt ostry 1) (√13)²=√26)²+(√5)²−2cos β⇔

	9		7
cosβ=		to sinβ=
	√130		√130

2)

	1		7
PΔ=		*√26*√5*
	2		√130

	7
PΔ=
	2

==========

Mila: Właśnie miałam napisać, że Eta "obrysuje" trójkąt.

Eta:

Mariusz: Mila gdyby uczeń przepisał twoje rozwiązanie to miałby za nie ucięte punkty i obniżoną ocenę (źle przepisałaś wzór cosinusów , jednak w linijce poniżej wartości funkcyj trygonometrycznych już są poprawnie więc wg mnie może to być policzone jako dwa błędy) Ula wspominała wzór Herona Na pierwszy rzut oka może się się wydawać on dobrym pomysłem bo mamy dane długości boków ale wymaga on wymnożenia czterech czynników z których każdy jest sumą trzech składników

Mila: Masz rację Mariuszu. Dziękuję Szkoda, że uczeń nie zainteresował się rozwiązaniami, może zauważyłby pomyłkę w zapisie a nie przepisał Poprawiam: (√13)²=(√26))²+(√5)²−2*√5*√26*cos β⇔

Eta:

	a2+c2−b2
cosβ=
	2ac

	5+26−13		9
cosβ=		=
	2√5*√26		√130

	7
sinβ=
	√130

Damian#UDM: Eta ten pomysł z prostokątem jest tak zajebisty, że aż zacznę go stosować Nigdy bym na to nie wpadł!

Mariusz: Tylko ciekawe czy zawsze uda ci się tak ładnie dobrać długości boków tego prostokąta

Damian#UDM: Mariuszu przypuszczam, że nie zawsze da się tak zrobić