trójkąt gemin: W trójkącie ABC kąt BAC=120^o , punkt M jest srodkiem boku BC Na bokach AB i AC wybrano odpowiednio punkty E i F tak że EB=CF=EF Wykaż że kąt EMF jest kątem prostym

30: US Skąd to zadanie?

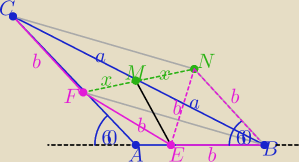
Eta: Na prostej FM odkładamy odcinek |MN|=|FM|=x więc czworokąt FBNC jest równoległobokiem ( bo M jest środkiem przekątnych BC i FN o kącie ostrym ABN=60^o to |BN|=|EB|=|CF|=b zatem ΔBEN jest równoboczny to ΔFEN jest równoramienny ⇒ ME jest jego wysokością⇒ ME⊥FM i mamy tezę |∡EMF|=90^o =============

Bogdan:

Eta: Poprawiam zapis: ........ to kąt ostry ABN=60^o ( zamiast "o kącie ostrym ABN=60^o" bo BN∥AC

Eta: Heeeeeeeeeeeeeeeeeeeeeeeeeeej Bogdan