czworokat US: Czworokąt ABCD jest wpisany w okrąg Na boku AB obrano punkt E tak,ze AE=DC Na bokuAD obrano punkt F tak że AF=BC Wykaż,że przekątna AC połowi odcinek EF

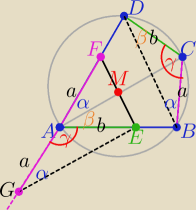
Eta: |AG|=|AF|=|CB| kąty α, β −− wpisane oparte na łukach DC , CB to ΔDCB≡ΔGAE z cechy ( bkb) bo kąt γ= 180^o−(α+β) −− z warunku wpisania czworokąta w okrąg zatem kąty AGE i DAC mają miarę α więc proste GE i AC są równoległe to z tw. Talesa

|FM|		|FA|
	=		= 1⇒ |FM|=|ME|
|ME|		|AG|

M jest środkiem odcinka FE c.n.w.

30: Skad to zadanie?

Eta: Ja nie wiem