matematykaszkolna.pl
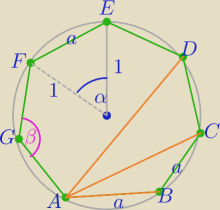
siedmiokat gonek: Siedmiokąt foremny ABCDEFG jest wpisany w okrąg jednostkowy. Pokaż że kwadraty długości odcinków AB, AC oraz AD są pierwiastkami równania x3−7x2+14x−7=0
30 lip 09:51
Iryt: rysunek Siedmiokąt foremny.
 2π 
1) α=
− kąt środkowy
 7 
Suma kątów wewnętrznych= (7−2)*π=5π
 5π 
β=
 7 
2)
 2π 2π 
|AB|2=a2=2−2cos
=2*(1−cos
)⇔
 7 7 
 2π 
x1=2*(1−cos
)
 7 
==============
 5π 
|AC|2=2a2−2*a2cosβ=2a2−2a2cos
 7 
 2π 2π 2π 
|AC|2=2a2*(1+cos
)=2*2*(1−cos
)*(1+cos
⇔
 7 7 7 
 2π 
x2=4*sin2
 7 
===============
 a2 
 2π 
2*(1−cos
)
 7 
 
|AD|2=
=
=
 
 π 
4sin2
 14 
 
 π 
4sin2
 14 
 
 
 2π 
(1−cos
)
 7 
 
 2π 
(1−cos
)
 7 
 
|AD|2=
=
 
 π 
1−cos
 7 
 
 π 
1−cos
 7 
 
 π 
x3=2*(1+cos
)
 7 
============ 4) Dalej spróbuj sam , możesz skorzystać z wzorów Viet'a .
30 lip 19:24
Iryt: Dalej podpowiedź:
 4π 3π 
x2=2*(1−cos
)=2*(1+cos
)
 7 7 
 1 
wartość : cos(pi/7)−cos(2pi/7)+cos(3pi/7) =
 2 
 1 
wartość : cos(pi/7)*cos(2pi/7) *cos(3pi/7)=
 8 
2 sie 18:19
Mila:
2sin(π/7)*cos(π/7)*cos(2π/7)]] *cos(3π/7) 
=
2sin(π/7) 
 sin(2π/7)*cos(2π/7)*cos(3π/7) 
=
=
 2sin(π/7) 
 sin(4π/7)*cos(3π/7) 
=
=
 4sin(π/7) 
 sin(3π/7)*cos(3π/7) sin(6π/7) 
=
=
=
 4sin(π/7) 8sin(π/7) 
 sin(π/7) 
=
=
 8sin(π/7) 
 1 
=
 8 
====
3 sie 19:22
Eta: A gonek i tak ma to............ emotka
3 sie 19:41
Mila: No cóż , "sorry, taki mamy klimat" emotka
3 sie 19:42
Eta: Mila wytłumacz mi ... |AD|2= ..... ( skąd to?
3 sie 19:43
Mila: |AD| skorzystałam z gotowego wzoru , ale potem obliczyłam z ΔDOA i nie chciało mi się pisać na nowoemotka
 6π π 
|AD|2=12+12−2*cos
=2*(1+cos
)
 7 7 
3 sie 20:30
Mila: Wzór 1 z ΔAED:
3 sie 20:36
Eta: No właśnie ( ja tak liczyłam)
 6π 
|∡DOA|=3α=
 7 
z tw. cosinusów w ΔAOD |AD|2=12+12−2*1*1*cos(6π/7) = 2(1+cos(π/7)) Nie rozumiałam skąd napisałaś
 a2 
|AD|2=
−− i o to pytałam
 4sin2(π/14) 
Dzięki emotka
3 sie 20:53
Mila:
 1 
wartość : cos(pi/7)−cos(2pi/7)+cos(3pi/7) =
 2 
1) 2sinx*cosy=sin(x+y)+sin (x−y), 2sinx*cosx=sin2x
 2π 5π 
−cos (
)=cos
 7 7 
2)
 π π 5π 3π 
2 sin
*(cos
+cos
+cos
)
 7 7 7 7 
 
=
 π 
2sin
 7 
 
 
 π π π 5π π 3π 
2 sin
*cos
+ 2 sin
*cos
+2 sin
*cos
 7 7 7 7 7 7 
 
=
=
 
 π 
2sin
 7 
 
 
 2π 6π 4π 4π 2π 
sin
+sin
+sin(−
)+sin
+sin(−
)
 7 7 7 7 7 
 
=
=
 
 π 
sin
 7 
 
 
 6π 
sin
 7 
 
=
=
 
 π 
2sin
 7 
 
 
 π 
sin
 7 
 1 
=
=
 
 π 
2 sin
 7 
 2 
==============
5 sie 23:03
Mariusz: Eta 3 sie 19:41 Możliwe że widział rozwiązanie tyle że nie odpisuje Może też się przydać innym , tym którzy mają podobne zadanie Gdyby chciał rozwiązywać to równanie trzeciego stopnia to otrzymałby pierwiastki także wyrażone za pomocą funkcyj trygonometrycznych tyle że ich argument dzielony byłby przez trzy a nie przez siedem No i trzeba by było zdefiniować funkcję odwrotną do funkcji trygonometrycznej
6 sie 10:45
Adamm: samo zadanie wydaje się interesujące ale użycie kątów w rozwiązaniu już mniej interesujące
6 sie 20:49
Mariusz: Adam rozwiązując to równanie dostaniesz zespolone pierwiastniki więc jeśli chcesz mieć rozwiązania wyrażone za pomocą funkcyj o argumentach rzeczywistych to jednak trzeba z trygonometrii skorzystać x3−7x2+14x−7=0
 7 7 49 343 
(x−
)3=x3−3(x2)
+3(x)
−
 3 3 9 27 
 7 49 343 
(x−
)3=x3−7x2+
x−
 3 3 27 
 7 7 7 49 343 7 49 
(x−
)3−
(x−
)=x3−7x2+
x−
−
x+
 3 3 3 3 27 3 9 
 7 7 7 196 
(x−
)3−
(x−
)=x3−7x2+14x−
 3 3 3 27 
 7 7 7 7 196 7 
(x−
)3−
(x−
)+
=x3−7x2+14x−
+
 3 3 3 27 27 27 
 7 7 7 7 
(x−
)3−
(x−
)+
=x3−7x2+14x−7
 3 3 3 27 
 7 
y=x−
 3 
 7 7 
y3−
y+
=0
 3 27 
y=u+v
 7 7 
(u+v)3−
(u+v)+
=0
 3 27 
 7 7 
u3+3u2v+3uv2+v3−
(u+v)+
=0
 3 27 
 7 7 
u3+v3+
+3(u+v)(uv−
)=0
 27 9 
 7 
u3+v3+
=0
 27 
 7 
3(u+v)(uv−
)=0
 9 
 7 
u3+v3+
=0
 27 
 7 
uv−
=0
 9 
 7 
u3+v3=−
 27 
 7 
uv=
 9 
 7 
u3+v3=−
 27 
 343 
u3v3=
 729 
 7 343 
t2+
t+
=0
 27 729 
 7 49 1372 
(t+
)2−
+
=0
 54 2916 2916 
 7 1323 
(t+
)2+
=0
 54 2916 
 7 21√3 7 21√3 
(t+
+
i)(t+
−
i)=0
 54 54 54 54 
 7 21√3 49+3*441 49+1323 
(
)2+(
)2=
=
 54 54 2916 2916 
 7 21√3 1372 
(
)2+(
)2=
 54 54 2916 
 14√7 
|z|=
 54 
 7√7 
|z|=
 27 
 √7 
|z|1/3=
 3 
 
21√3 
54 
 
Arg(z)=arctan(
)
 
 7 
−
 54 
 
Arg(z)=π−arctan(3√3) gdzie arctan to funkcja odwrotna do tangensa
 7 21√3 7 21√3 
(−
+
i)1/3+(−
−
i)1/3=
 54 54 54 54 
√7 1 1 
(cos(
(π−arctan(3√3)))+isin(
(π−arctan(3√3))))
3 3 3 
 √7 1 1 
+
(cos(−
(π−arctan(3√3)))+isin(−
(π−arctan(3√3))))
 3 3 3 
√7 1 √7 1 
cos(
(π−arctan(3√3)))+
isin(
(π−arctan(3√3)))
3 3 3 3 
 √7 1 √7 1 
+
cos(
(π−arctan(3√3)))−
isin(
(π−arctan(3√3)))
 3 3 3 3 
 2√7 1 
=
cos(
(π−arctan(3√3)))
 3 3 
Pierwiastki trzeciego stopnia z
 7 21√3 
−
−
i
 54 54 
oraz
 7 21√3 
−
+
i
 54 54 
należy tak dobrać aby spełniony był układ równań
 7 
u3+v3=−
 27 
 7 
uv=
 9 
√7 1 √7 1 
cos(
(π−arctan(3√3)))+
isin(
(π−arctan(3√3)))
3 3 3 3 
 √7 1 √7 1 
+
cos(
(π−arctan(3√3)))−
isin(
(π−arctan(3√3)))
 3 3 3 3 
 2√7 1 
=
cos(
(π−arctan(3√3)))
 3 3 
 7 2√7 1 
x−
=
cos(
(π−arctan(3√3)))
 3 3 3 
 7 2√7 1 
x=
+
cos(
(π−arctan(3√3)))
 3 3 3 
Pozostałe pierwiastki to
√7 1 √7 1 
cos(
(3π−arctan(3√3)))+
isin(
(3π−arctan(3√3)))
3 3 3 3 
 √7 1 √7 1 
+
cos(
(3π−arctan(3√3)))−
isin(
(3π−arctan(3√3)))
 3 3 3 3 
 2√7 1 
=
cos(
(3π−arctan(3√3)))
 3 3 
 7 2√7 1 
x−
=
cos(
(3π−arctan(3√3)))
 3 3 3 
 7 2√7 1 
x=
+
cos(
(3π−arctan(3√3)))
 3 3 3 
 7 2√7 1 
x=
+
cos(π−
arctan(3√3))
 3 3 3 
 7 2√7 1 
x=
−
cos(
arctan(3√3))
 3 3 3 
√7 1 √7 1 
cos(
(5π−arctan(3√3)))+
isin(
(5π−arctan(3√3)))
3 3 3 3 
 √7 1 √7 1 
+
cos(
(5π−arctan(3√3)))−
isin(
(5π−arctan(3√3)))
 3 3 3 3 
 2√7 1 
=
cos(
(5π−arctan(3√3)))
 3 3 
 7 2√7 1 
x−
=
cos(
(5π−arctan(3√3)))
 3 3 3 
 7 2√7 1 
x=
+
cos(
(5π−arctan(3√3)))
 3 3 3 
 7 2√7 5 1 
x=
+
cos(
π−
arctan(3√3))
 3 3 3 3 
 7 2√7 π 1 
x=
+
cos(2π−(
+
arctan(3√3)))
 3 3 3 3 
 7 2√7 π 1 
x=
+
cos((
+
arctan(3√3)))
 3 3 3 3 
 7 2√7 1 
x=
+
cos(
(π+arctan(3√3)))
 3 3 3 
Gdybyśmy chcieli rozwiązywać to równanie to otrzymalibyśmy rozwiązania w następującej postaci
 7 2√7 1 
x1=
+
cos(
(π−arctan(3√3)))
 3 3 3 
 7 2√7 1 
x2=
−
cos(
arctan(3√3))
 3 3 3 
 7 2√7 1 
x3=
+
cos(
(π+arctan(3√3)))
 3 3 3 
7 sie 11:02