równoległobok kamper: W równoległoboku ABCD z wierzchołka kąta D rozwartego poprowadzono prostą która przecięła przekątną AC i bok BC oraz przedłużenie boku AB odpowiednio w punktach K, L,M tak,że pola trójkątów BML i KCL są równe W jakim stosunku punkt K dzieli przekątną AC ?

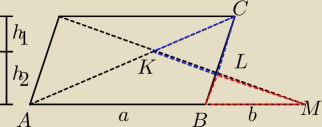
wredulus_pospolitus: P_ΔKLC = P_ΔBML −−−> P_ΔABC = P_ΔAMK −−−>

	a		h2		|AK|
−−−> a*(h1+h2) = (a+b)*h2 −−−> ah1 = bh2 −−−>		=		=
	b		h1		|CK|

Eta:

a
	= ? −−− konkretnie !
b

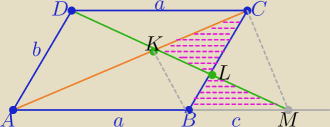Eta: 1/ z równości pól z treści zadania ⇒ CM∥BK, czworokąt BMCK jest trapezem

	|AK|
2/ szukany stosunek k=
	|KC|

zatem

	|AB|		|DC|		|LC|		|CM|
k=		=		=		=		=
	|BM|		|BM|		|LB|		|KB|

	|AC|		|AK|+|KC|		1		1
=		=		= 1+		więc k=1+		i k>0
	|AK|		|AK|		k		k

k²−k−1=0 Δ=5

	1+√5
k=
	2

	|AK|		1+√5		|KC|		√5−1
to		=		lub		=
	|KC|		2		|AK|		2

=============================

Eta: A kamper ma to.......... ( pewnie odpoczywa na Mazurach Ciekawe czy poda odpowiedź( ze zbiorku) do tego zadania