równanie marcus: Dane jest równanie 3x²(x+2)=1 którego pierwiastkami rzeczywistymi są liczby a,b,c

	1		1		1
Oblicz wartość wyrażenia		+		+
	a4		b4		c4

Eta: 72

Mila: Wzory Viete'a.

Damian#UDM: 3x²(x+2)=1 → 3x³+6x²−1=0 → ax³ + bx² + cx + d =0 a=3, b=6, c=0, d=−1

⎧	a+b+c=−2
⎨	ab+ac+bc=0
⎩	abc=13

1		1		1		(ac)4 + (bc)4 + (ab)4
	+		+		=		=
a4		b4		c4		(abc)4

= 81*[(ac)⁴ + (bc)⁴ + (ab)⁴] Co dalej?

wredulus_pospolitus: x⁴ + y⁴ + z⁴ = (x² + y² + z²)² − 2(x²y² + x²z² + y²z²) = = ( (x+y+z)² − 2(xy + xz + yz) )² − 2(x²y² + x²z² + y²z²) = = ( (ac + bc + ab)² − 2(ab²c + a²bc + abc²) )² − 2(a²b²c⁴ + a⁴b²c² + a²b²c⁴) = = ( (ac + bc+ab)² − 2abc(a+b+c) )² − 2(abc)²*(a² + b² + c²) = = ( (ac + bc+ab)² − 2abc(a+b+c) )² − 2(abc)²*( (a+b+c)² − 2(ab + ac + bc) ) = ... wzory Viete'a Jedyne z czego korzystamy (i to wielokrotnie) to ze wzoru skróconego mnożenia: (x+y+z)² = x² + y² + z² + 2xy + 2xz + 2yz

Eta: Taka podpowiedź

	1		1
3x2(x+2)=1 ⇒		=3(x+2) ⇒		=9(x+2)2
	x2		x4

zatem

	1		1		1
		+		+		= 9[(a+2)2+(b+2)2+(c+2)2]=....
	a4		b4		c4

i działaj dalej.........

ICSP: (ac)⁴ + (bc)⁴ + (ab)⁴ = = [(ac)² + (bc)² + (ab)²]² − 2[(abc²)² + (a²bc)² + (ab²c)²] = = ([ac + bc + ab]² − 2(abc)²[a + b + c])² − 2(abc)[(a+b+c)² − 2(ab + bc + ac)] =

	16		8		7
=		−		=
	9		9		9

	1		1		1		7
W =		+		+		= 81 *		= ...
	a4		b4		c4		9

Eta:

Mariusz: 1. Sprowadzasz do wspólnego mianownika 2. Wyrażasz funkcję symetryczną w liczniku za pomocą sumy iloczynów funkcji symetrycznych podstawowych 3. Korzystasz ze wzorów Vieta

1		1		1		b4c4+a4c4+a4b4
	+		+		=
a4		b4		c4		a4b4c4

Rozkład na sumę iloczynów funkcji symetrycznych podstawowych wygląda następująco b⁴c⁴+a⁴c⁴+a⁴b⁴= (((ab+ac+bc)⁴−4(abc)(ab+ac+bc)²(a+b+c)+2(abc)²(a+b+c)²+4(abc)²(ab+ac+bc))) a+b+c=−2 ab+ac+bc=0

	1
abc=
	3

	1		1		1
b4c4+a4c4+a4b4=04−4*		*02*(−2)+2*(		)2(−2)2+4*(		)2*0
	3		3		3

	8
b4c4+a4c4+a4b4=
	9

	1
(abc)4=
	81

	8   9		8
=		=		*81
	1   81		9

=8*9=72

Eta:

Mariusz: Do poczytania http://matwbn.icm.edu.pl/ksiazki/mon/mon11/mon1109.pdf

Eta: Wolą czytać ........ "365 dni"

Mila: Damian, dalej tak: 3x²(x+2)=1 3x³+6x−1=0 a+b+c=−2 ab+ac+bc=0

	1
a*b*c=
	3

========= 1) ab+ac+bc=0 /:(abc)

1		1		1
	+		+		=0 /2
c		b		a

2)

1		1		1		1		1		1
	+		+		+2*(		+		+		)=0
a2		b2		c2		ab		ac		bc

1		1		1		c+b+a
	+		+		+2*		=0⇔
a2		b2		c2		abc

1		1		1
	+		+		+2*(−2)*3=0
a2		b2		c2

3)

1		1		1
	+		+		=12 /2
a2		b2		c2

1		1		1		1		1		1
	+		+		+2*(		+		+		)=144
a4		b4		c4		a2b2		a2c2		b2c2

1		1		1		c2+b2+a2
	+		+		+2*		=144
a4		b4		c4		a2*b2*c2

1		1		1		(a+b+c)2−2*(ab+ac+bc)
	+		+		+2*		=144
a4		b4		c4		(a*b*c)2

1		1		1
	+		+		+2*(−2)2*9=144
a4		b4		c4

1		1		1
	+		+		=144−72
a4		b4		c4

========================= Trochę długo

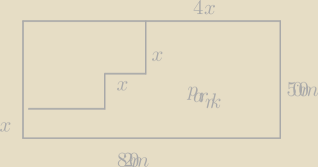
janko: Proszę o pomoc. W obrębie prostokątnego parku należy wyznaczyć obszar chroniony, jak na rys. Jakie wartości może przyjmować x? Wyznacz te wartości5 x, dla których obszar chroniony jest mniejszy od 207000 m²

wredulus_pospolitus: ten 'środkowy' x dotyczy którego boku 'górnego' czy 'prawego' czy jednego i drugiego

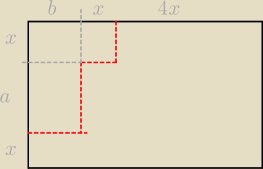
wredulus_pospolitus: a + 2x = 500 b + 5x = 800 x² + (a+x)*b < 207'000

wredulus_pospolitus: wyznaczamy z dwóch pierwszych równań 'a' i 'b' i podstawiamy do nierówności. wyznaczamy możliwe wartości 'x' ... pamiętaj w jakim zakresie może być 'x'