Dla chętnych Minato: Hejka, na wakacyjną nudę proponuję zadanko Zad1 Udowodnij, że dla dodatnich liczb a, b, c zachodzi nierówność √a²+1 + √b²+1 + √c²+1 ≥ √(a+b+c)²+9

ICSP: jest to nic innego jak nierówność : ||x + y + z|| ≤ ||x|| + ||y|| + ||z|| dla wektorów : x = [a,1] , y = [b,1] , z = [c,1]

Minato: ICSP brawo, ale raczej nikłe są szanse na przedstawienie takiego rozwiązania przez licealistę. Ale łatwo Twoje rozwiązanie przetransferować na łatwiejsze dla ucznia rozumowanie

ICSP: Najpierw pokazać nierówność trójkąta: √a² + 1 + √b² + 1 ≥ √(a+b)² + 2 a następnie wykorzystać ją do pokazania tezy?

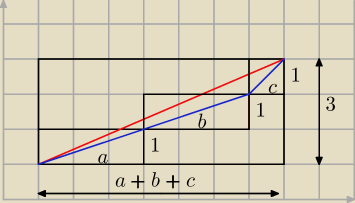
Minato: Interpretacja geometryczna

Des: Można tak [ ( √a²+1 +√b²+1 ) + √c²+1 ]² ≥ (a+b+c)²+9 ( √a²+1 +√b²+1 )² + 2√c²+1(√a²+1 +√b²+1) + c²+1 ≥ (a+b+c)²+9 a²+1+2√(a²+1)(b²+1)+b²+1+2√c²+1(√a²+1 +√b²+1)+c²+1 ≥ a²+2ab+b²+2c(a+b)+c²+9 √(a²+1)(b²+1) + √(c²+1)(a²+1) + √(c²+1)(b²+1) ≥ ab + 1 + ac + 1 + bc + 1 Wystarczy wykazać, że: √(a²+1)(b²+1) ≥ ab + 1 ⋀ √(c²+1)(a²+1) ≥ ac + 1 ⋀ √(c²+1)(b²+1) ≥ bc +1 a to już łatwo