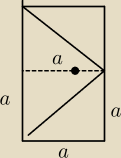
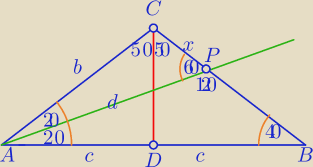
 |AP|=d, |CP|=x
1) W ΔCDB:
|AP|=d, |CP|=x
1) W ΔCDB:
| c | ||
sin50o= | ⇔c=bsin50o | |
| b |
| 1 | 1 | 2bsin2oo | |||
d*x*sin60o= | *b*d*sin20o stąd: x= | ||||
| 2 | 2 | √3 |
| 1 | 1 | 2bsin100o | |||
d*x*sin60o= | x*b*sin100o stąd: d= | ||||
| 2 | 2 | √3 |
| 2bsin20o | 2bsin100o | |||
3) x+d= | + | = | ||
| √3 | √3 |
| 2b | 2b | |||
= | *(sin20o+sin100o)= | *2 sin 60o*cos400= | ||
| √3 | √3 |
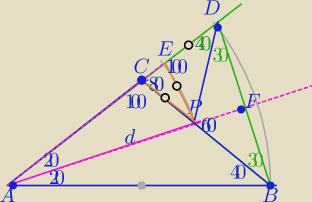 Bez trygonometrii.
1) Przedłużam AC w taki sposób, aby |AD|=AB|
ΔABD− Δrównoramienny, AF− symetralna BD
E− tak zaznaczone, aby |AE|=AP|
ΔAPE− Δrównoramienny, kąty przy podstawie EP mają po 80 o
2) ΔCPE− Δrównoramienny,
|CP|=|EP|
3) |PD|=|PB| i kąty w ΔBDP są równe jak na rysunku (zaznaczone zielonym kolorem)⇒
ΔPED−Δrównoramienny i |ED|=|EP|=|CP|⇒
|AD|=|CE|+|ED|=|AP|+|CP|=|AB|
Bez trygonometrii.
1) Przedłużam AC w taki sposób, aby |AD|=AB|
ΔABD− Δrównoramienny, AF− symetralna BD
E− tak zaznaczone, aby |AE|=AP|
ΔAPE− Δrównoramienny, kąty przy podstawie EP mają po 80 o
2) ΔCPE− Δrównoramienny,
|CP|=|EP|
3) |PD|=|PB| i kąty w ΔBDP są równe jak na rysunku (zaznaczone zielonym kolorem)⇒
ΔPED−Δrównoramienny i |ED|=|EP|=|CP|⇒
|AD|=|CE|+|ED|=|AP|+|CP|=|AB|
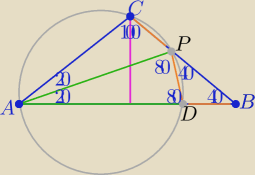 3 sposób
Na boku AB obieram taki punkt D ,że |AP|=|AD|
to trójkąt ADP równoramienny o kątach ADP=APD=80o
oraz kąty DBP=DPB=40o to trójkąt DBP też równoramienny
Na czworokącie ADPC da się opisać okrąg
to |DP|=|CP|=|DB|
i mamy tezę:
|AP|+|CP|=|AP|+|DB|=|AB|
=====================
3 sposób
Na boku AB obieram taki punkt D ,że |AP|=|AD|
to trójkąt ADP równoramienny o kątach ADP=APD=80o
oraz kąty DBP=DPB=40o to trójkąt DBP też równoramienny
Na czworokącie ADPC da się opisać okrąg
to |DP|=|CP|=|DB|
i mamy tezę:
|AP|+|CP|=|AP|+|DB|=|AB|
=====================