punkty supernat: Z 25 punktów na płaszczyźnie, których obie współrzędnie należą do zbioru {−2,−1, 0, 1, 2}, wybrano 17 punktów. Pokaż że wśród tych 17 punktów istnieją trzy które nie są współliniowe takie że jeden z nich jest środkiem odcinka utworzonego przez dwa pozostałe.

wredulus_pospolitus: sprawdź treść zadania ... jak punkty mają NIE BYĆ współliniowe, a jednocześnie jeden z nich ma być ŚRODKIEM odcinka utworzonego przez dwa pozostałe (czyli punkty mają być współliniowe)

supernat: Bez słowa "nie" Z 25 punktów na płaszczyźnie, których obie współrzędnie należą do zbioru {−2,−1, 0, 1, 2}, wybrano 17 punktów. Pokaż że wśród tych 17 punktów istnieją trzy które są współliniowe takie że jeden z nich jest środkiem odcinka utworzonego przez dwa pozostałe.

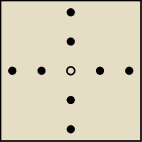
Adamm: Ponieważ 16/5 = 3, reszty 1, to jeśli takich punktów współliniowych nie ma, to musi to wyglądać jak na rysunku. Widać dlaczego 17 nie działa. Np. w wierszach musiałby być drugi taki wiersz jak ten środkowy.

Adamm: Czyli nie tylko znajdą się współliniowe, ale współliniowe i równoległe do osi