kombinatoryka
tok: Na planszy o wymiarach 8×8 ułożono jeden klocek o wymiarach 1×1. Okazało się, że pozostałe pola
można szczelnie przykryć lockami o wymiarach 1 × 3 (klocki można obracać w taki sposób, że
klocki nie nachodz¡ na siebie i nie wystaj¡ poza planszę. Wskaż wszystkie pola planszy, na
których może leżeć kocek 1 × 1.
16 lip 22:42
Blee:
Tak dokładnie wygląda treść zadania, czy po prostu chcesz się tego dowiedzieć, ale sama treść
zadania wygląda z gola inaczej?
Bo jeżeli tak dokładnie wygląda treść zadania to jest to bardziej zadanie logiczne niż
sprawdzające znajomość materiału z działu kombinatoryki, ale skoro tak jest to:
Plansze można podzielić na 8 przystających części. Zauważmy ze w każdej tej części (trójkącie)
mamy odpowiadające sobie pola. Związku z tym wystarczy sprawdzić sytuację dla pół z jednego
tego obszaru (10 pól) aby mieć sprawdzone dla całej planszy.
Problemem jest to że powinno się udowodnić ze dane pole nie może być tym polem, a wątpię byście
mieli robić coś takiego.
17 lip 07:42
tok: Jejku, na na prawdę nie rozumiem dalej. Czy mógłbyś to wyjaśnić jakoś prościej?

17 lip 13:14
Blee:
Ale czego nie rozumiesz? Pytałem się jaka DOKLADNIE jest treść zadania
17 lip 15:22
tok: Taka, jak dokładnie napisałem.
17 lip 16:31
an:
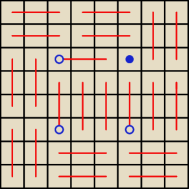
17 lip 23:58
wredulus_pospolitus:
@an −−− jedyne co pokazałeś/−aś to to, że te cztery punkty są możliwymi miejscami gdzie klocek
1x1 mógł się znajdować .. nie jest to jednoznaczny dowód, że nie ma innych miejsc na tej
planszy. <−−− i w tym tkwi cały problem
18 lip 00:01

