geometria foxy: Dany jest trójkąt ABC, w którym kACB = 60◦. Na trójk¡cie tym opisano okrąg o. Punkt X jest środkiem tego łuku BC okręgu o, który nie zawiera punktu A, a punkt Y jest środkiem tego łuku CA okręgu o, który nie zawiera punktu B. Wykaż, że prosta XY jest styczna do okręgu wpisanego w trójkąt ABC.

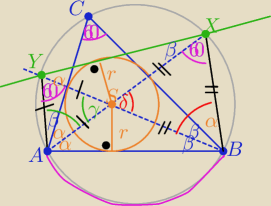
Eta: 1/ rysunek i odpowiednie zgodne z treścią oznaczenia 2/ skoro X i Y są środkami łuków ⇒ proste AX i BY są dwusiecznymi kątów przy wierzchołkach A i B Punkt S przecięcia dwusiecznych jest środkiem okręgu wpisanego w ΔABC Z tw. o kątach wpisanych opartych na tych samych łukach ( zaznaczone na rysunku) i mamy dwa trójkąty równoboczne : BXS : i AYS bo α+β=60^o zatem ΔABS i XYS są przystające z cechy (bkb) więc odległości punktu S od boków zarówno AB jak i XY są równe "r" co daje tezę Prosta XY jest styczna do okręgu wpisanego w ΔABC