dowód polo: W trójkącie ABC, ∡BAC=2∡CBA, CD dwusieczna kąta BCA. Wykaż że BC = AC + AD.

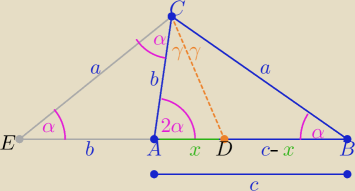
Eta: Odkładamy bok "b" na przedłużeniu BA ( otrzymujemy trójkąt równoramienny ACE 1/ ΔACE i ΔBCE są podobne z cechy (kkk)

	a		b
to		=		⇒ a2−b2=bc
	b+c		a

2/ z tw. o dwusiecznej w ΔABC

	b		a
		=		⇒ bc=(a+b)*x
	x		c−x

łącząc (1) i (2) otrzymujemy tezę: (a−b)(a+b)=(a+b)*x ⇒a=b+x |BC|=|AC|+|AD| ============== c.n.w.