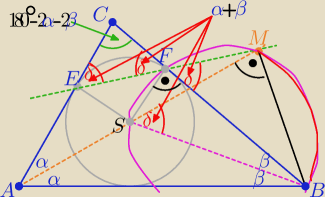
 δ=|∡BSM|=α+β −− miara kata zewnętrznego ΔABS
ΔCEF równoramienny ( z tw. o odcinkach stycznych
to |∡EFC|=|∡BFM|=δ=α+β
zatem na czworokącie BMFS da się opisać okrąg (bo kąty δ wpisane oparte na łuku BM
to na łuku BS oparte są kąty BFS i BMS
i mamy tezę
|∡BFS|=90o( ze styczności) = |∡BMS|=90o
ΔBMS −− jest prostokątny
c.n.w.
δ=|∡BSM|=α+β −− miara kata zewnętrznego ΔABS
ΔCEF równoramienny ( z tw. o odcinkach stycznych
to |∡EFC|=|∡BFM|=δ=α+β
zatem na czworokącie BMFS da się opisać okrąg (bo kąty δ wpisane oparte na łuku BM
to na łuku BS oparte są kąty BFS i BMS
i mamy tezę
|∡BFS|=90o( ze styczności) = |∡BMS|=90o
ΔBMS −− jest prostokątny
c.n.w.