Geometria an: Dany jest trójkąt ABC. Wykaż, że odbicie ortocentrum trójkąta ABC względem środka boku AB leży na okręgu opisanym na trójkącie ABC.

Eta: Łatwy ten dowód

an: To sarkazm? Mógłbym jakąś wskazówkę?

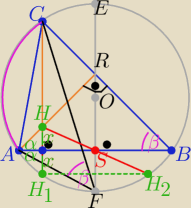
Eta: Przeanalizuj to co podałam na rysunku i dodaj odpowiednie komentarze.. H₂∊ o(O,R) c.n.w.

an: Dlaczego u Ciebie spodek wysokości AR leży na średnicy? Moim zdaniem nie musi tak być

Eta: Nie leży ! (choć może) i jego położenie nie ma znaczenia w tym dowodzie

Eta: R −− dł. Promienia okręgu opisanego ( R−− nie jest spodkiem wysokości

an: Czy mógłbym prosić o drobną podpowiedź odnośnie kątów α? gdzie one dokładnie lezą i z czego to wynika

Eta: 1/ kąty AH₁C i AFC i ABC −− mają równe miary β bo są wpisane i oparte na tym samym łuku AC w Δ BAM (prostokątnym) M spodek wysokości poprowadzonej z wierzchołka A to kąt BAM= α ΔAH₁N też prostokątny ( N −− środek odcinka HH₁ bo kąt H_AN = α więc H₁ symetryczny do H względem prostej AB następnie H₂ symetryczny do H₁ względem średnicy EF okręgu Złożenie dwóch symetrii osiowych o osiach prostopadłych AB i EF i przecinających się w punkcie S jest symetrią środkową względem punktu S zatem HS=SH₂ a to oznacza ,że H₂ jest odbiciem H względem środka S boku AB czyli H₂ należy do okręgu opisanego na trójkącie ABC co kończy dowód