trójkąt mati: W okrąg o promieniu R i środku S wpisano trójkąt ABC, następnie w trójkąt ABC wpisano okrąg o środku O i promieniu r Dwusieczna kąta ACB przecina w punkcie P okrąg opisany na tym trójkącie Wykaż że |OC|*|OP|=2Rr

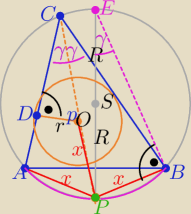
Eta: Ładne zadanko Skąd masz to zadanie ? 1/ rysunek i oznaczenia zgodne z treścią |EP|=2R i |OD|=r ΔPBE i ΔCDO odobne z cechy (kkk) , bo są prostokątne i γ −− kąty wpisane oparte na łuku BP |BP|=|AP|=|OP|=x −−− z tw. o "trójliściu" ( możesz poczytać o nim na Wiki więc z podobieństwa

r		|OC|
	=
|BP|		|EP|

r		|OC|
	=
OP|		2R

i mamy tezę: |OP|*|OC|=2Rr =============