Krzywa, równanie
szk: Jaką krzywą przedstawia równanie: y2−4y+6x−2=0
Próbowałem dopełnić do kwadratu zupełnego w igreku, ale wyszło mi tylko coś takiego:
(y2−4y+4)=6−6x
(y−2)2=6−6x
|y−2|=√6−6x, co chyba nie jest dobrą drogą i nie o to tutaj chodzi
Jakaś wskazówka w jaki inny sposób to uporządkować/wyrazić?
6 lip 21:46
Mila:
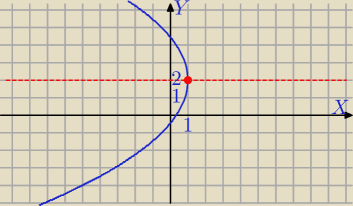
1) (y−2)
2=6−6x⇔
(y−2)
2=−6*(x−1)
Wsp. wierzchołka paraboli : W=(1,2)
y=2− oś symetrii paraboli
2) Możesz też przedstawić równanie w takiej postaci:
y
2−4y+6x−2=0
6x=−y
2+4y+2
| | 1 | | 2 | | 1 | |
x=− |
| y2+ |
| y+ |
| parabola o poziomej osi symetrii |
| | 6 | | 3 | | 3 | |
3) Do narysowania możesz wykorzystać:
y=2±
√6−6x
6 lip 22:37
Szkolniak: Jeśli wyrażamy to w ten sposób jaki jest w punkcie drugim (chodzi mi o to, że po lewej stronie
równania mamy 'x', a nie 'y'), to czy nie powinniśmy w sumie zamienić miejscami współrzędnych
tego wierzchołka?
Swoja drogą, postać w drugim punkcie zdecydowanie bardziej mi odpowiada − w pierwszym punkcie
nie wiem w sumie skąd wiadomo, że równość '(y−2)2=−6(x−1)' przedstawia parabolę.
6 lip 22:56
Mila:
To jest równanie kanoniczne paraboli o poziomej osi symetrii.
7 lip 00:14
Szkolniak: | | 1 | | 1 | |
(y−2)2=−6(x−1) ⇔ − |
| (y−2)2=x−1 ⇔ x=− |
| (y−2)2+1 |
| | 6 | | 6 | |
Rzeczywiście, dziękuje
A spytam przy okazji o drugi przykład, gdzie równanie ma postać:
7x
2+7y
2−2xy−48x−48y+144=0
Doszedłem do takiej postaci:
(x−y)
2+6x
2+6y
2−48x−48y+144=0
(x−y)
2+6(x
2−8x+16)−96+6(y
2−8y+16)−96=−144
(x−y)
2+6(x−4)
2+6(y−4)
2=48
Dobry trop?
7 lip 00:26
7 lip 02:08
7 lip 02:40
7 lip 02:42
jc:
7(x−4)
2 + 7(y−4)
2 − 2(x−4)(y−4) = 48
3(x+y−8)
2 + 4(x−y)
2=48
| (x+y−8)2 | | (x−y)2 | |
| + |
| =1 i teraz jest jasne, że to elipsa |
| 16 | | 12 | |
Środek leży w punkcie (4,4), elipsa leży pod kątem 45 stopni
osie mają długości:
√8,
√6
7 lip 10:03
Szkolniak: Na razie ten drugi przykład to dla mnie magia, spróbuję posiedzieć nad tym tematem − dziękuję
7 lip 21:29
Mila:
7x2+7y2−2xy−48x−48y+144=0
Na razie takimi krzywymi nie zajmuj się.
W tym przykładzie należy się "pozbyć" wyrazu (−2xy) stosując przekształcenie izometryczne−
w tym przypadku obrót układu współrzędnych.
Jeżeli koniecznie chcesz dojść do rozwiązania podanego przez JC
( który wszystko widzi bez liczenia),
to pomogę.
8 lip 16:10
Szkolniak: Właśnie chcialem poszukać w internecie jakichś przykładów odnośnie takich zadań, ale jakoś
niczego nie mogłem znaleźć na ten temat, czegoś, co byłoby dobrze wyjaśnione.
A wyjaśnienie jak do tego dojść chyba nie ma sensu, bo i tak nic mi to nie da − na ten moment
nie potrafię nawet odpowiednio odczytać tego zapisu podanego przez jc.
8 lip 18:11
8 lip 23:38
Szkolniak: Qulka dziękuje! wieczorem przejrzę jak będzie czas
9 lip 14:39
https://www.wolframalpha.com/input/?i=+7x%5E2%2B7y%5E2%E2%88%922xy%E2%88%9248x%E2%88%9248y%2B144%3D0