losowanie
tyber: Spośród wierzchołków 12tokata foremnego wybrano losowo cztery. Oblicz prawdopodobieństwo że te
punkty są wierzchołkami trapezu równoramiennego.
6 lip 20:05
Qulka: mi wychodzi 130/495
6 lip 23:21
tyber: A jak policzyc te sprzyjające?
7 lip 07:57
a7:
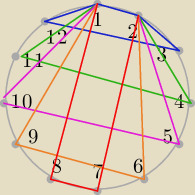
1 2 3 12 12 trapezów
1 2 4 11 12 trapezów
12 5 10 12 trapezów
1 2 7 8 12 trapezów
1 3 4 12 12 trapezów
reszta trapezów się powtarza

Ω=12*11*10*9=11880
P(A)=60/11880=1/198
7 lip 09:39
a7: chyba trochę za małe to prawdopodobieństwo mi wyszło......
7 lip 09:41
a7: jeszcze 1 2 6 9 12 trapezów
| | 1 | |
wtedy P(A) byłoby równe |
| |
| | 165 | |
7 lip 09:45
a7: jeszcze kolejność dowolna czyli 72*4!=72*24=1728
wtedy P(A)=8/55
7 lip 09:59
ite:
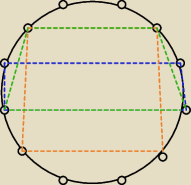
Witaj
a7, takich trapezów jest więcej.
7 lip 09:59
ite: Część narysowanych przez mnie nie pokazała się na rysunku (czyli jeszcze nie wszystko tu
działa).
7 lip 10:02
a7: Witaj
ite 
, no nic przynajmniej spróbowałam...
7 lip 10:02
ite: To powtórz takie liczenie jak 09:39. Zaczęłaś dla górnej podstawy o końcach 1 i 2, to dalej
końce 12 i 3, a potem podstawa 11 i 4.
7 lip 10:06
a7: ale właśnie nie rozumiem, bo wydaje mi się, że oprócz kwadratowych trapezów (których będzie 3?)
wszystkie już się powtarzają

7 lip 10:13
a7: czyli aktualnie wychodzi mi 75*4!=1800 P(A)=1800/11880=5/33
7 lip 10:17
ite: U Ciebie 09:39 wierzchołkami górnej podstawy są sąsiednie wierzchołki dwunastokąta a dolną
podstawę stanowią odpowiednie pary pozostałych. Ja dalej tworzę kolejne trapezy o górnych
podstawach równoległych do odcinka o wierzchołkach 1 i 2 (i dolnych podstawach różnych od 7 i
8, żeby nie liczyć po dwa razy tych samych).
12,3,4,11
12,3,5,10
7 lip 10:22
a7: to może jeszcze 1 4 6 11 12 trapezów
czyli 87*4!=2088 wtedy P(A)=2088/11880=29/165
7 lip 10:24
a7: widzę te różne trapezy 12,3,4,11 i 12,3,5,10 ale nie umiem ich policzyć.........
7 lip 10:29
a7:
ok, chyba mam czyli
72 trapezy z 9:39 plus
3 trapezy 12,3,6,9 plus
12,3,4,11 12 trapezów
12,3,5,10 12 trapezów
razem 99*4!=2376
P(A)=2376/11880=1/5
7 lip 10:45
a7: 
7 lip 10:45
a7: rysunek mi się nie wysłał
7 lip 10:46
a7: znikł
7 lip 10:47
ite:
Rysunki nadal znikają : (
Niestety muszę wracać do pracy i nie mam czasu dalej liczyć. Mam nadzieję, że pojawi się
Qulka i napisze, jak to rozwiązywała.
7 lip 10:51
a7: tak, zobaczymy....
7 lip 10:54
ite:
1/ z tych 6 odcinków wybieramy po 2 różne → są to podstawy trapezów
2/ potem ilość trapezów razy sześć (bo pierwszy odcinek może się zaczynać od wierzchołka
1,2,3,4,5,6, potem mamy znów ten sam zestaw odcinków)
chyba tak można to obliczyć
7 lip 11:49
ite: i rysunek zniknął
7 lip 11:49
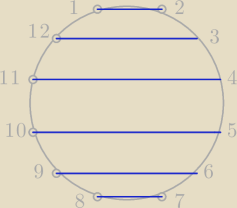
ite:
7 lip 11:52
a7: to Twoim sposobem
ite mamy P(A)=90/1350=1/15


7 lip 12:04
a7: oj nie,coś jeszcze źle......
7 lip 12:06
ite: | | | |
Wszystkich czworokątów jest | =495 i tu się zgadza z zapisem Qulki. |
| | |
Ze wszystkich wierzchołków wybieramy po cztery, one tworzą czworokąt tylko w jeden sposób
(rosnąco ułożone numerami).
7 lip 12:43
Pytający:
Ite, dobrze kombinujesz. Jeszcze rozpatrz sytuacje analogiczne do tej, gdy jednym z
odcinków (z których wybierasz podstawy trapezu) jest odcinek 1−3. Tu też jest możliwych 6
różnych orientacji tych odcinków i w każdym przypadku wyboru dokonujesz spośród 5 odcinków
równoległych.
| | | | 150 | | 30 | |
Znaczy wg mnie odpowiedź to: |
| = |
| = |
| . |
| | | | 495 | | 99 | |
| | | | 150 | |
Albo nieco inaczej liczone: |
| = |
| |
| | | | 495 | |

7 lip 12:57
Qulka: liczyłam na piechotę
https://prnt.sc/tdce9y
do odcinka AB mam 5 trapezów, AC 4 AD 5 AE 4 AF 5
..4...5...4..5..4...5..
do BC 4..3..4..3..4..3..4.3..4..3..4..
CD 3..2..3...
więc potem dodałam znów o 1 mniej aż do zera
30+20 + 24+15 + 18+10 + 12+5 + 6 = 50+39+28+17+6 = 140
oo na koniec w dodawaniu trochę nie wyszło

7 lip 13:27
Jerzy:
Zgadzam się w 100% z rozwiązaniem Pytającego
7 lip 13:47
Qulka: 6•5+5•4 to miałam czyli dobry początek

ale potem eliminacja powtórek pewnie nie do końca mi wyszła

7 lip 14:01
tyber: Wynik sie zgadza pytajacy

7 lip 14:12
ite: Dzięki za wyjaśnienia : )
Gdyby ilość wierzchołków była nieparzysta, to nie trzeba by było sumować tych dwóch przypadków?
7 lip 15:21
Pytający:
Tak, Ite. Wtedy dla każdej możliwej orientacji odcinków równoległych jest tyle samo.
7 lip 17:58
ite: dziękuję!
8 lip 09:16
Pytający:
| | 135 | |
Moja poprzednia odpowiedź jest błędna, poprawna odpowiedź to |
| . |
| | 495 | |
W poprzednim rozumowaniu zabrakło rozpatrzenia tego, kiedy otrzymujemy prostokąty. W przypadku
otrzymania prostokąta policzony on został jako 2 różne trapezy prostokątne, gdyż na 2 sposoby
można wybrać, która para boków stanowi podstawy trapezu. Oczywiście taki prostokąt powinien
zostać policzony jednokrotnie.
A prostokątów jest (oznaczenia jak na rysunku
Qulki:
https://prnt.sc/tdce9y ):
• 6 podobnych do ABGH,
• 6 podobnych do ACGI,
• 3 podobnych do ADGJ.
8 lip 18:12
 1 2 3 12 12 trapezów
1 2 4 11 12 trapezów
12 5 10 12 trapezów
1 2 7 8 12 trapezów
1 3 4 12 12 trapezów
reszta trapezów się powtarza
1 2 3 12 12 trapezów
1 2 4 11 12 trapezów
12 5 10 12 trapezów
1 2 7 8 12 trapezów
1 3 4 12 12 trapezów
reszta trapezów się powtarza  Ω=12*11*10*9=11880
P(A)=60/11880=1/198
Ω=12*11*10*9=11880
P(A)=60/11880=1/198

 Witaj a7, takich trapezów jest więcej.
Witaj a7, takich trapezów jest więcej.
 , no nic przynajmniej spróbowałam...
, no nic przynajmniej spróbowałam...







 ale potem eliminacja powtórek pewnie nie do końca mi wyszła
ale potem eliminacja powtórek pewnie nie do końca mi wyszła
