zadania Eta: WAKACYJNE ZMAGANIA( dla chętnych) z "ulubioną" PLANIMETRIĄ Tu możecie wrzucać ciekawe zadania ( może przydadzą się przyszłym maturzystom): zad1 Wewnątrz czworokąta wypukłego ABCD o polu P obrano punkt M x,y,z.w,−−− odległości punktu M od wierzchołków tego czworokąta Wykaż,że x+y+z+w≥ 2√2P

zuza: o co chodzi z tym punktem P pod pierwiastkiem?

zuza: A nie to pole sory

qwas: w+x+y+z≥AC+BD≥2√AC*BD≥2√2P

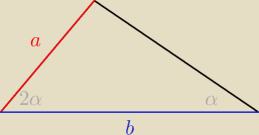
Saizou : To ja podrzucę. zad2 Wykazać, że b<3a. PS. Oczekiwana metoda bez trygonometrii, ale można też z jej wykorzystaniem

Eta: Dzięki Saizou za podjęcie tematu Pozdrawiam

Saizou : W końcu odzyskałem kolorowy nick wiec można szaleć Dzięki za Miłych wakacji

qwas: Saizouczy ten alfa jest dowolny?

Saizou : dla α∊(0, 60°)

9marca: b<3a |:a b/a<3 z tw sin b/a=sin(180−3α)/sinα=3−4sin²α<3

Saizou : a bez trygonometrii?

Eta:

alojz: Wenatrz równoległoboku ABCD obrano punkt P taki że ∡PAD=∡ PCD. Wykaz ze dwusieczne kątów ∡ BAD oraz ∡BPD są równoległe.

Wolfus: Jakoś umarło......

daras:

Kacper: Eta rozwiązałaś to poprzednie? nie wyświetla mi się

Eta: @Kacper Które?

Kacper: To od Saizou

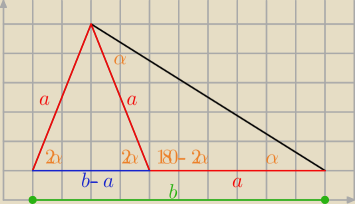
Minato: Nierówność trójkąta a+a > b−a 3a > b Na zdrowie zawodusie

Eta: